當前位置：試卷中心 > 試卷詳情

2008年湖南省岳陽市臨湘市九年級學科知識競賽（暨奧賽班招生）數學試卷

發布：2024/11/11 4:0:2

一、選擇題（共10小題，每小題3分，滿分30分）

1．實數a在數軸上的對應點與原點的距離等于3，實數b滿足b+7=0，則
7
（
-
b
+
2
-
a
）
（
-
-
b
+
2
-
a
）
2
ab
的值等于（　　）
A．-
3
2
或
3
2
B．-6或6 C．0 D．6
組卷：110引用：1難度：0.9
解析
2．若a＜b＜0，化簡
3
（
a
-
b
）
3
-
（
a
-
b
）
2
+
a
2
-
b
2
的結果是（　　）
A．a-b B．-2a C．2b D．3（a-b）
組卷：92引用：1難度：0.9
解析
3．若α、β是方程x²-x-2006=0的兩個實數根，則α+β²的值是（　　）
A．1 B．2007 C．-1 D．2006
組卷：133引用：2難度：0.9
解析
4．關于m的不等式組
2
（
m
-
1
）
3
-
5
m
+
1
2
≥
-
3
3
m
-
2
（
m
-
1
）
≥
a
的非正整數解是-3，-2，-1，0，則a的最大值為（　　）
A．-3 B．0 C．1 D．-1
組卷：244引用：1難度：0.9
解析
5．已知a＜-1，點（a-1，y₁），（a,y₂），（a+1，y₃）都在函數y=x²的圖象上，則（　　）
A．y₁＜y₂＜y₃ B．y₁＜y₃＜y₂ C．y₃＜y₂＜y₁ D．y₂＜y₁＜y₃
組卷：1101引用：49難度：0.9
解析
6．如圖菱形ABCD中，EF∥AB，FG∥AD，BF：FD=m：n,CD=15，則EF+FG的長為（　　）
A．mn
B．15
C．6m+9n
D．不能確定，但與m、n的取值有關
組卷：106引用：1難度：0.9
解析
7．△ABC中，AB=13，AC=12，BC=5，點O為AB的中點，以O為圓心、OA為半徑作圓O，將△ABC繞點O旋轉90°后，此時點C與圓O的位置關系是（　　）
A．點C在圓O上 B．點C在圓O外 C．點C在圓O內 D．不能確定
組卷：73引用：1難度：0.7
解析
8．如圖中，BC切圓O于B，AB=BC=OA，連AC交圓O于D，OC交圓O于E，則∠CED的度數為（　　）
A．105° B．112.5° C．150° D．97.5°
組卷：86引用：1難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共6小題，滿分58分）

23．如圖，矩形ABCD中，AD＜AB，P、Q分別為AD、BC的中點．N為DC上的一點，△AND沿直線AN對折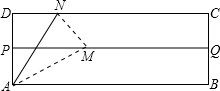，點D恰好與PQ上的M點重合．若AD、AB分別為方程x²-6x+8=0的兩根．
（1）求△AMN的外接圓的直徑；
（2）四邊形ADNM有內切圓嗎？有則求出內切圓的面積，沒有請說明理由．
組卷：216引用：1難度：0.1
解析
24．已知拋物線y=x²+4ax+3a²（a＞0）
（1）求證：拋物線的頂點必在x軸的下方；
（2）設拋物線與x軸交于A、B兩點（點A在點B的右邊），過A、B兩點的圓M與y軸相切，且點M的縱坐標為
3
，求拋物線的解析式；
（3）在（2）的條件下，若拋物線的頂點為P，拋物線與y軸交于點C，求△CPA的面積．
組卷：122引用：1難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2008年湖南省岳陽市臨湘市九年級學科知識競賽（暨奧賽班招生）數學試卷

一、選擇題（共10小題，每小題3分，滿分30分）

1．實數a在數軸上的對應點與原點的距離等于3，實數b滿足b+7=0，則7（-b+2-a）（--b+2-a）2ab的值等于（ ）

2．若a＜b＜0，化簡3（a-b）3-（a-b）2+a2-b2的結果是（ ）

3．若α、β是方程x2-x-2006=0的兩個實數根，則α+β2的值是（ ）

4．關于m的不等式組2（m-1）3-5m+12≥-33m-2（m-1）≥a的非正整數解是-3，-2，-1，0，則a的最大值為（ ）

5．已知a＜-1，點（a-1，y1），（a,y2），（a+1，y3）都在函數y=x2的圖象上，則（ ）

6．如圖菱形ABCD中，EF∥AB，FG∥AD，BF：FD=m：n,CD=15，則EF+FG的長為（ ）

7．△ABC中，AB=13，AC=12，BC=5，點O為AB的中點，以O為圓心、OA為半徑作圓O，將△ABC繞點O旋轉90°后，此時點C與圓O的位置關系是（ ）

8．如圖中，BC切圓O于B，AB=BC=OA，連AC交圓O于D，OC交圓O于E，則∠CED的度數為（ ）

三、解答題（共6小題，滿分58分）

1．實數a在數軸上的對應點與原點的距離等于3，實數b滿足b+7=0，則
7
（
-
b
+
2
-
a
）
（
-
-
b
+
2
-
a
）
2
ab
的值等于（　　）

2．若a＜b＜0，化簡
3
（
a
-
b
）
3
-
（
a
-
b
）
2
+
a
2
-
b
2
的結果是（　　）

3．若α、β是方程x²-x-2006=0的兩個實數根，則α+β²的值是（　　）

4．關于m的不等式組
2
（
m
-
1
）
3
-
5
m
+
1
2
≥
-
3
3
m
-
2
（
m
-
1
）
≥
a
的非正整數解是-3，-2，-1，0，則a的最大值為（　　）

5．已知a＜-1，點（a-1，y₁），（a,y₂），（a+1，y₃）都在函數y=x²的圖象上，則（　　）

6．如圖菱形ABCD中，EF∥AB，FG∥AD，BF：FD=m：n,CD=15，則EF+FG的長為（　　）

7．△ABC中，AB=13，AC=12，BC=5，點O為AB的中點，以O為圓心、OA為半徑作圓O，將△ABC繞點O旋轉90°后，此時點C與圓O的位置關系是（　　）

8．如圖中，BC切圓O于B，AB=BC=OA，連AC交圓O于D，OC交圓O于E，則∠CED的度數為（　　）