當前位置：試卷中心 > 試卷詳情

2022-2023學年安徽省滁州二中、定遠三中高二（上）月考數學試卷（12月份）

發布：2024/7/11 8:0:9

1．已知i為虛數單位，z為復數，集合P={1，-1}，Q={i,i²}，若P∩Q={zi}，則復數z等于（　　）
A．-i B．i C．-1 D．1
組卷：0引用：1難度：0.9
解析
2．已知數列{a_n}的通項公式a_n=（-1）ⁿ⁺¹+1，則a₂+a₃=（　　）
A．-1 B．0 C．1 D．2
組卷：98引用：4難度：0.8
解析
3．
|
e
|
=
1
是向量
e
為單位向量的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：57引用：3難度：0.8
解析
4．已知cos（
π
2
+α）=
1
2
，α∈（-
π
2
，0），則tanα等于（　　）
A．-
3
B．
3
C．-
3
3
D．
3
3
組卷：48引用：2難度：0.7
解析
5．已知圓C₁：x²+y²-4x-2y-5=0，圓C₂：x²+y²+2x-2y-14=0，則兩圓的位置關系是（　　）
A．相離 B．相交 C．內含 D．相切
組卷：290引用：3難度：0.8
解析
6．設函數
f
（
x
）
=
（
a
-
2
）
x
,
（
x
≥
2
）
（
1
2
）
x
-
1
，
（
x
＜
2
）
，
a
n
=
f
（
n
）
，若數列{a_n}是單調遞減數列，則實數a的取值范圍為（　　）
A．（-∞，2） B．（-∞，
13
8
]
C．（-∞，
7
4
） D．
[
13
8
，
2
）
組卷：98引用：14難度：0.7
解析
7．若雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線與直線y=2x垂直，且直線3x-y+6=0過雙曲線的一個焦點，則雙曲線實軸長為（　　）
A．
2
2
B．
2
3
C．
8
5
5
D．
4
5
5
組卷：236引用：5難度：0.8
解析

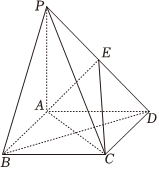21．在如圖所示的四棱錐P-ABCD中，四邊形ABCD為矩形，PA⊥平面ABCD，E為PD的中點．
（1）證明：PB∥平面ACE；
（2）若PA=AD=1，AB=2，求平面EAC與平面ACD夾角的余弦值．
組卷：61引用：3難度：0.4
解析
22．已知橢圓C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的離心率為
2
2
3
，點F₁，F₂是橢圓C的左、右焦點，點P是C上任意一點，若△PF₁F₂面積的最大值為
4
2
．
（1）求橢圓C的標準方程；
（2）直線l₁：
y
=
1
3
x
與橢圓C在第一象限的交點為M，直線l₂：
y
=
1
3
x
+
m
（
m
≠
0
）
與橢圓C交于A，B兩點，連接MA，MB，與x軸分別交于P，Q兩點，求證：△MPQ始終為等腰三角形．
組卷：54引用：4難度：0.6
解析

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

1．已知i為虛數單位，z為復數，集合P={1，-1}，Q={i,i2}，若P∩Q={zi}，則復數z等于（ ）