2023-2024學年湖北省宜昌市宜都一中高二（上）期中數學試卷

一、單選題：本大題共8小題，每小題5分，共計40分。每小題給出的四個選項中，只有一個選項是正確的。請把正確的選項填涂在答題卡相應的位置上。

• 1．已知

  a

  =

  （

  1

  ，

  2

  ，

  1

  ）

  ，

  b

  =

  （

  -

  2

  ，

  3

  ，

  1

  ）

  ，則

  （

  a

  +

  b

  ）

  ?

  b

  =（　　）

  A．-19

  B．-20

  C．20

  D．19
  組卷：144引用：4難度：0.7

  解析

• 2．在空間直角坐標系中，點（-2，1，4）關于平面Oxy對稱的點坐標是（　　）

  A．（-2，1，-4）

  B．（2，1，-4）

  C．（-2，-1，-4）

  D．（2，-1，4）
  組卷：17引用：3難度：0.8

  解析

• 3．從裝有除顏色外完全相同的2個紅球和2個白球的口袋內任取2個球，那么對立的兩個事件是（　　）

  A．至少有1個白球，至少有1個紅球

  B．至少有1個白球，都是紅球

  C．恰有1個白球，恰有2個白球

  D．至少有1個白球，都是白球
  組卷：924引用：7難度：0.7

  解析

• 4．已知一組數據從小到大為4，5，6，8，m,13，18，30，若這組數據的80%分位數是中位數的兩倍，則m=（　　）

  A．12

  B．11

  C．10

  D．9
  組卷：231引用：6難度：0.7

  解析

• 5．已知直線l₁：x+2ay-1=0與直線l₂：（3a-1）x-ay-1=0平行，則a=（　　）

  A．0

  B．0或 - 1 6

  C． 1 6

  D．0或 1 6
  組卷：49引用：3難度：0.7

  解析

• 6．已知方程x²+y²-4x+2y+a=0表示圓，則實數a的取值范圍是（　　）

  A．（5，+∞）

  B．（-5，+∞）

  C．（-∞，5）

  D．（-∞，1）
  組卷：117引用：6難度：0.7

  解析

• 7．兩定點A，B的距離為3，動點M滿足|MA|=2|MB|，則M點的軌跡長為（　　）

  A．4π

  B． 2 3 π

  C． 2 2 π

  D．2π
  組卷：57引用：6難度：0.6

  解析

四、解答題：本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知點P和非零實數λ，若兩條不同的直線l₁，l₂均過點P，且斜率之積為λ，則稱直線l₁，l₂是一組“P_λ共軛線對”，如直l₁：y=2x,l₂：

  y

  =

  -

  1

  2

  x

  是一組“O_-1共軛線對”，其中O是坐標原點．
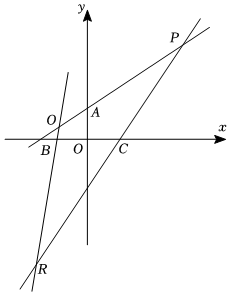
  （1）已知點A（0，1）、點B（-1，0）和點C（1，0）分別是三條直線PQ，QR，RP上的點（A，B，C與P，Q，R均不重合），且直線PR，PQ是“P₁共軛線對”，直線QP，QR是“Q₄共軛線對”，直線RP，RQ是“R₉共軛線對”，求點P的坐標；
  （2）已知點

  Q

  （

  -

  1

  ，-

  2

  ）

  ，直線l₁，l₂是“Q_-2共軛線對”，當l₁的斜率變化時，求原點O到直線l₁，l₂的距離之積的取值范圍．
  組卷：94引用：3難度：0.5

  解析

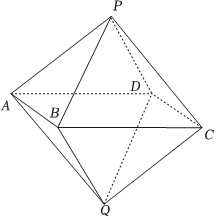• 22．如圖，在八面體PABCDQ中，四邊形ABCD是邊長為2的正方形，平面PAD∥平面QBC，二面角P-AB-C與二面角Q-CD-A的大小都是30°，

  AP

  =

  CQ

  =

  3

  ，PD⊥AB．
  （1）證明：平面PCD∥平面QAB；
  （2）設G為△QBC的重心，是否在棱PA上存在點S，使得SG與平面ABCD所成角的正弦值為

  30

  20

  ，若存在，求S到平面ABCD的距離，若不存在，說明理由．
  組卷：143引用：6難度：0.5

  解析