2022-2023學年天津一中高三（上）第三次月考數學試卷

一.選擇題：本題共9小題，每小題5分，共45分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x∈Z|

  3

  1

  -

  x

  ∈Z}，B={x∈Z|x²-x-6≤0}，則A∪B=（　　）

  A．{2}	B．{-2，0，2}
  C．{-2，-1，0，1，2，3，4}	D．{-3，-2，0，2，4}
  組卷：64引用：3難度：0.8

  解析

• 2．若a,b,c為非零實數，則“a＞b＞c”是“a+b＞2c”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：220引用：6難度：0.8

  解析

• 3．已知a=log₂0.8，b=2^0.1，c=sin2.1，則（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．c＜a＜b

  D．b＜c＜a
  組卷：93引用：2難度：0.8

  解析

• 4．函數f（x）=

  x

  -

  sinx

  x

  2

  +

  1

  的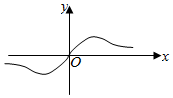圖象大致為（　　）

  A．	B．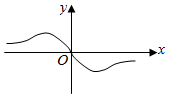
  C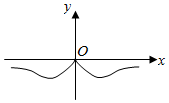．	D．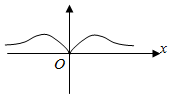
  組卷：343引用：9難度：0.7

  解析

• 5．已知F₁、F₂分別為雙曲線E：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  的左、右焦點，點M在E上，|F₁F₂|：|F₂M|：|F₁M|=2：3：4，則雙曲線E的漸近線方程為（　　）

  A．y=±2x

  B．y=± 1 2 x

  C．y= ± 3 x

  D．y= ± 3 3 x
  組卷：721引用：4難度：0.8

  解析

• 6．設S_n是等比數列{a_n}的前n項和，若S₃=4，a₄+a₅+a₆=6，則

  S

  9

  S

  6

  =（　　）

  A． 3 2

  B． 19 10

  C． 5 3

  D． 19 6
  組卷：1639引用：14難度：0.7

  解析

三、解答題：本大題共5小題，共75分.解答應寫出文字說明，證明過程或演算步驟.

• 19．已知等差數列{a_n}的前n項和為S_n，且S₅=45，a₂+3a₄=40．數列{b_n}的前n項和為T_n，滿足3T_n+1=4b_n．
  （1）求數列{a_n}、{b_n}的通項公式；
  （2）若

  c

  n

  =

  b

  n

  （

  3

  a

  n

  -

  2

  ）

  a

  n

  ?

  a

  n

  +

  1

  ，求數列{c_n}的前n項和R_n；
  （3）設

  d

  n

  =

  S

  n

  b

  n

  ，求證：

  n

  ∑

  k

  =

  1

  d

  k

  ＜

  8

  -

  n

  +

  4

  2

  n

  -

  1

  ．
  組卷：48引用：1難度：0.5

  解析

• 20．已知函數f（x）=e^xcosx,g（x）=acosx+x（a＜0），曲線y=g（x）在

  x

  =

  π

  6

  處的切線的斜率為

  3

  2

  ．
  （1）求實數a的值；
  （2）對任意的

  x

  ∈

  [

  -

  π

  2

  ，

  0

  ]

  ，

  tf

  （

  x

  ）

  -

  g

  ′

  （

  x

  ）

  ≥

  0

  恒成立，求實數t的取值范圍；
  （3）設方程f（x）=g'（x）在區間

  （

  2

  nπ

  +

  π

  3

  ，

  2

  nπ

  +

  π

  2

  ）

  （

  n

  ∈

  N

  +

  ）

  內的根從小到大依次為x₁，x₂，…，x_n，…，求證：x_n+1-x_n＞2π．
  組卷：213引用：3難度：0.2

  解析