2022-2023學年安徽省池州市貴池區高一（下）期中數學試卷

一、單選題（每題5分，共40分）

• 1．已知復數

  z

  =

  2

  +

  i

  1

  +

  i

  ，則

  z

  的虛部為（　　）

  A． 1 2

  B． 1 2 i

  C． - 1 2

  D． - 1 2 i
  組卷：245引用：9難度：0.9

  解析

• 2．如圖，已知等腰三角形△O'A'B'，O'A'=A'B'是一個平面圖形的直觀圖，斜邊O'B'=2，則這個平面圖形的面積是（　　）

  A． 2 2

  B．1

  C． 2

  D． 2 2
  組卷：711引用：28難度：0.8

  解析

• 3．某圓錐的側面展開圖扇形的弧長為8π，扇形的半徑為5，則圓錐的體積為（　　）

  A．25π

  B．75

  C． 5 5 π

  D．16π
  組卷：85引用：5難度：0.7

  解析

• 4．已知

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  2

  ，

  e

  是與向量

  b

  方向相同的單位向量，向量

  a

  在向量

  b

  上的投影向量為

  -

  e

  ，則

  a

  與

  b

  的夾角為（　　）

  A．45°

  B．60°

  C．120°

  D．135°
  組卷：70引用：3難度：0.7

  解析

• 5．一正四棱柱的底面邊長為2，高為4，則該正四棱柱的外接球的表面積為（　　）

  A．6π

  B．12π

  C． 8 6 π

  D．24π
  組卷：12引用：3難度：0.7

  解析

• 6．已知△ABC的三個內角A，B，C所對的邊分別為a,b,c.若2cosCsinB=sinA，則該三角形的形狀是（　　）

  A．等邊三角形

  B．等腰三角形

  C．等腰三角形或直角三角形

  D．直角三角形
  組卷：103引用：8難度：0.7

  解析

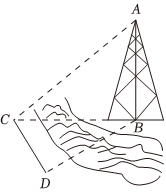• 7．如圖，測量河對岸的塔高AB時，可以選取與塔底B在同一水平面內的兩個測量基點C與D．現測得∠BCD=α，∠BDC=β，CD=s,在點C測得塔頂A的仰角為θ，則塔高AB=（　　）

  A． s ? tanθsinβ sin （ α + β ）	B． s ? tanθsin （ α + β ） sinβ
  C． s ? sinθsin （ α + β ） sinβ	D． s ? sinθsinβ sin （ α + β ）
  組卷：79引用：6難度：0.5

  解析

四、解答題（共70分）

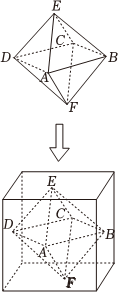• 21．如圖，兩個相同的正四棱錐底面重合組成一個八面體，可放入一個底面為正方形的長方體內，且長方體的正方形底面邊長為2，高為4，已知重合的底面與長方體的正方形底面平行，八面體的各頂點均在長方體的表面上．
  （Ⅰ）若點A，B，C，D恰為長方體各側面中心，求該八面體的體積；
  （Ⅱ）求該八面體表面積S的取值范圍．
  組卷：72引用：4難度：0.4

  解析

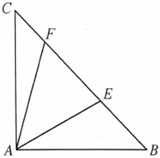• 22．如圖，某小區有一塊空地△ABC，其中AB=50，AC=50，∠BAC=90°，小區物業擬在中間挖一個小池塘△AEF，E，F在邊BC上（E，F不與B，C重合，且E在B，F之間），且

  ∠

  EAF

  =

  π

  4

  ．
  （1）若

  BE

  =

  10

  2

  ，求EF的值；
  （2）為節省投入資金，小池塘△AEF的面積需要盡可能的小．設∠EAB=θ，試確定θ的值，使得△AEF的面積取得最小值，并求出△AEF面積的最小值．
  組卷：614引用：9難度：0.3

  解析