2021-2022學年江西省初中名校聯盟九年級（下）開學數學試卷

一、選擇題（本大題共6小題，每小題3分，共18分。每小題只有一個正確選項）

• 1．如果3a=2b（ab≠0），那么比例式中正確的是（　　）

  A． a b = 3 2

  B． b a = 2 3

  C． a 2 = b 3

  D． a 3 = b 2
  組卷：438引用：16難度：0.9

  解析

• 2．下列圖形中，是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：156引用：4難度：0.9

  解析

• 3．關于函數y=-

  2

  x

  ，下列說法中錯誤的是（　　）

  A．函數的圖象在第二、四象限

  B．函數的圖象與坐標軸沒有交點

  C．y的值隨x值的增大而減小

  D．函數的圖象關于原點對稱
  組卷：644引用：5難度：0.8

  解析

• 4．關于x的一元二次方程kx²+3x-1=0有實數根，則k的取值范圍是（　　）

  A．k≤- 9 4

  B．k≤- 9 4 且k≠0

  C．k≥- 9 4

  D．k≥- 9 4 且k≠0
  組卷：7882引用：91難度：0.9

  解析

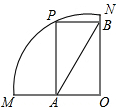• 5．如圖，四邊形PAOB是扇形OMN的內接矩形，頂點P在

  ?

  MN

  上，且不與點M，N重合，數學學習小組在探究時得出以下結論：
  ①PB+PA是定值；
  ②當點P是

  ?

  MN

  的中點時，四邊形PAOB是正方形；
  ③當點P在

  ?

  MN

  上移動時，矩形PAOB的大小隨之變化，但AB的長度不變；
  ④連接MP，PN，若

  ?

  MP

  =2

  ?

  PN

  ，則MP=2PN．
  以上結論正確的序號是（　　）

  A．①②④

  B．②③④

  C．②③

  D．①②③④
  組卷：369引用：1難度：0.6

  解析

• 6．已知二次函數y=-3x²+12x-9與直線y=m,以下說法不正確的是（　　）

  A．若方程-3x2+12x-9=m有實數根，則m≤3

  B．若二次函數y=-3x2+12x-9與直線y=m交于點E，F，若EF=6，則m=-24

  C．若x1，x2（x1＜x2）是方程-3x2+12x-9=m（m＜0）的兩個根，則x1＜1＜3＜x2

  D．二次函數y=-3x2+12x-9-m的圖象實質是將二次函數y=-3x2+12x-9的圖象向上平移m個單位長度，其中關于x的方程-3x2+12x-9-m≤0的解是y=-3x2+12x-9與y=m的交點的橫坐標
  組卷：106引用：1難度：0.5

  解析

二、填空題（本大題共6小題，每小題3分，共18分）

• 7．已知二次函數y=-x²+2x-5，用配方法化為y=a（x-h）²+k的形式是y=

  ．
  組卷：240引用：2難度：0.6

  解析

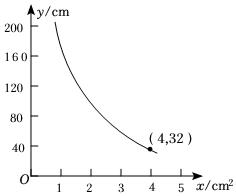• 8．在制作拉面的過程中，用一定體積的面團做拉面，面條的總長度y（單位：cm）與面條的橫截面積x（單位：cm²）成反比例函數關系，其圖象如圖所示，當面條的橫截面積為0.4cm²時，則面條總長度是

  cm.
  組卷：126引用：1難度：0.7

  解析

五、（本大題共2小題，每小題9分，共18分）

• 23．已知二次函數L：y=mx²+2mx-3（m≠0）．
  （1）以下有關二次函數L的性質結論序號正確的有

  ．
  ①二次函數的開口向上；
  ②二次函數的對稱軸是直線x=-1；
  ③二次函數的圖象經過定點（0，-3）和（-2，-3）；
  ④函數值y隨著x的增大而減小．
  （2）若二次函數L：y=mx²+2mx-3的圖象關于點（m,0）中心對稱得到二次函數G的圖象，則稱這兩個二次函數關于點（m,0）成對稱拋物線．
  ①直接寫出二次函數G的解析式．
  ②若拋物線G的頂點縱坐標y與橫坐標x之間存在一個函數關系式H，求出這個函數關系式；若二次函數L與函數H的圖象有交點，請直接寫出m的取值范圍．
  組卷：211引用：2難度：0.1

  解析

六、（本大題共12分）

• 24．在四邊形ABCD中，點G是DC上的點，連接BG，點F是BG上的點，在BC上取點H，使CG=CH，連接HF，CF，AF．
  （1）若四邊形ABCD為正方形．
  ①如圖1，點F為對角線AC上一點，求證：GF=FH；
  ②如圖2，若CF⊥BG于點F，求證：∠CFH=∠AFB．
  （2）如圖3，若四邊形ABCD為菱形，∠CFB=∠BCD，寫出∠BHF與∠FAB之間的數量關系．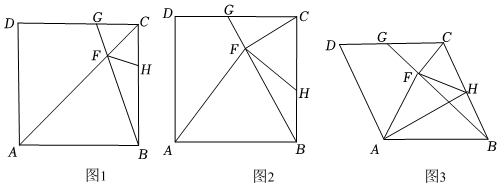
  
  組卷：28引用：1難度：0.2

  解析