2022-2023學年湖南省新高考教學教研聯盟高一（下）聯考數學試卷（5月份）

一、選擇題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．設集合A={y|y=3^x，x∈R}，B={x|x²＜4}，則A∩B=（　　）

  A．（-2，2）

  B．（0，2）

  C．（-2，+∞）

  D．（0，+∞）
  組卷：21引用：2難度：0.7

  解析

• 2．已知函數

  f

  （

  x

  ）

  =

  cos

  （

  2

  x

  +

  π

  3

  ）

  ，則下列結論錯誤的是（　　）

  A．f（x）的最小正周期為π

  B．f（x）的圖象關于直線 x = π 3 對稱

  C．f（x）的一個零點為 x = π 12

  D．f（x）在區間 （ 0 ， π 2 ） 上單調遞減
  組卷：118引用：2難度：0.7

  解析

• 3．如果一組數據x₁，x₂，x₃，?，x_n的方差是2，那么另一組數據5x₁+1，5x₂+1，5x₃+1，?，5x_n+1的方差為（　　）

  A．11

  B．20

  C．50

  D．51
  組卷：66引用：1難度：0.8

  解析

• 4．已知向量

  a

  與

  b

  的夾角為

  5

  π

  6

  ，且

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  3

  ，則

  a

  在

  b

  方向上的投影向量是（　　）

  A． 1 3 b

  B． - 2 3 a

  C． - 3 3 b

  D． - 1 3 b
  組卷：73引用：4難度：0.8

  解析

• 5．已知定義在R上的奇函數f（x）滿足：當x≥0時，f（x）=log₂（x+2）+x+b,則|f（x）|≥8的解集為（　　）

  A．（-∞，-6]∪[6，+∞）	B．（-∞，-4]∪[4，+∞）
  C．[-6，6]	D．[-4，4]
  組卷：105引用：2難度：0.5

  解析

• 6．記函數f（x）=sin（ωx+

  π

  6

  ）（ω＞0）的最小正周期為T，若

  π

  4

  ＜T＜

  π

  2

  ，且f（x）≤|f（

  π

  3

  ）|，則ω=（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：186引用：4難度：0.7

  解析

• 7．很多人的童年都少不了折紙的樂趣，如今傳統意義上的手工折紙已經與數學聯系在一起，并產生了許多需要縝密論證的折紙問題．有一張矩形紙片ABCD，BC=4，Q為BC的中點，將△ABQ和△DCQ分別沿AQ，DQ翻折，使點B與點C重合于點P，若∠APD=90°，三棱錐P-QAD的所有頂點都在球O的表面上，則球O的表面積為（　　）

  A．10π

  B．16π

  C．20π

  D．40π
  組卷：34引用：1難度：0.5

  解析

四、解答題

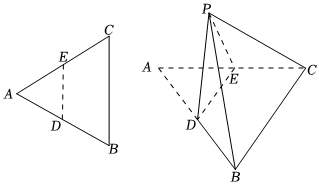• 21．如圖，已知△ABC是邊長為4的等邊三角形，D、E分別是AB、AC的中點，將△ADE沿著DE翻折，使點A到點P處，得到四棱錐P-BCED．
  （1）若

  PC

  =

  10

  ，證明：平面PDE⊥平面BCED；
  （2）若PB⊥PC，求直線PB與平面BCED所成角的正弦值．
  組卷：75引用：2難度：0.5

  解析

• 22．已知函數f（x）=2x²-ax+3，g（x）=4^x-2^x-a，a∈R．
  （1）若f（sinx）（x∈R）的最大值為6，求a的值；
  （2）當a＜0時，設

  h

  （

  x

  ）

  =

  f （ x ） ， x ＞ a

  g （ x ） ， x ≤ a

  ，若h（x）的最小值為

  -

  1

  2

  ，求實數a的值．
  組卷：29引用：2難度：0.5

  解析