2022-2023學年北京市懷柔區高二（上）期末數學試卷

一、選擇題共10小題，每小題4分，共40分。在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．已知直線l的傾斜角為

  π

  3

  ，則直線l的斜率為（　　）

  A． - 3

  B． 3

  C． - 3 3

  D． 3 3
  組卷：126引用：1難度：0.9

  解析

• 2．若直線2x+y-1=0與直線x-my=0垂直，則m=（　　）

  A．-2

  B． - 1 2

  C．2

  D． 1 2
  組卷：217引用：2難度：0.9

  解析

• 3．已知拋物線C：x²=4y,則焦點坐標為（　　）

  A． （ 1 16 ， 0 ）

  B． （ 0 ， 1 16 ）

  C．（1，0）

  D．（0，1）
  組卷：117引用：1難度：0.8

  解析

• 4．若點A（1，2，3），點B（4，-1，0），且

  AC

  =

  2

  CB

  ，則點C的坐標為（　　）

  A．（3，0，1）	B．（2，1，2）
  C． （ 3 2 ，- 3 2 ，- 3 2 ）	D． （ 5 2 ， 1 2 ， 3 2 ）
  組卷：904引用：4難度：0.8

  解析

• 5．若圓O₁：x²+y²=r²與圓O₂：（x-2）²+y²=9相內切，則r為（　　）

  A．1

  B．2

  C．5

  D．1或5
  組卷：205引用：3難度：0.8

  解析

• 6．將單位圓x²+y²=1上所有點的橫坐標變為原來的3倍，再將縱坐標變為原來的2倍，得到的曲線方程為（　　）

  A．9x2+4y2=1

  B． x 2 9 + 4 y 2 = 1

  C． x 2 9 + y 2 4 = 1

  D． 9 x 2 + y 2 4 = 1
  組卷：107引用：1難度：0.6

  解析

• 7．已知雙曲線C：x²-

  y

  2

  b

  2

  =1（b＞0）的離心率是2，則其漸近線的方程為（　　）

  A． x ± 3 y = 0

  B． 3 x ± y = 0

  C．x±3y=0

  D．3x±y=0
  組卷：268引用：3難度：0.7

  解析

三、解答題共6小題，共85分。解答應寫出文字說明，演算步驟或證明過程。

• 20．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點分別為F₁，F₂，且|F₁F₂|=4，且a=

  2

  b.
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）過點F₁的直線l與橢圓C交于A，B兩個不同的點，求證：x軸上存在定點P，使得直線PA與直線PB的斜率之和為零．
  組卷：398引用：4難度：0.3

  解析

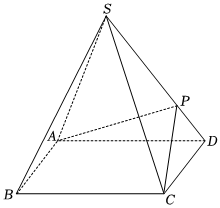• 21．如圖，四棱錐S-ABCD的底面是正方形，每條側棱的長都是底面邊長的

  2

  倍，P為側棱SD上的點．
  （Ⅰ）求證：AC⊥SD；
  （Ⅱ）若SD⊥平面PAC，求二面角P-AC-D的大小；
  （Ⅲ）在（Ⅱ）的條件下，側棱SC上是否存在一點E，使得BE∥平面PAC．若存在，求SE：EC的值；若不存在，試說明理由．
  組卷：170引用：2難度：0.6

  解析