2022年廣東省惠州市惠陽區八校聯考中考數學模擬試卷

一、選擇題（本大題共10小題，在每小題給出的四個選項中只有一項是符合題目要求的）

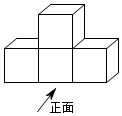• 1．如圖所示的幾何體是由4個相同的小正方體搭成的，它的主視圖是（　　）

  A．

  B．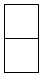

  C．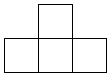

  D．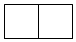
  組卷：79引用：4難度：0.8

  解析

• 2．化簡m+n-（m-n）的結果為（　　）

  A．2m

  B．-2m

  C．2n

  D．-2n
  組卷：761引用：88難度：0.9

  解析

• 3．一個密閉不透明的盒子里有若干個白球，在不許將球倒出來數的情況下，為了估計白球數，小剛向其中放入了8個黑球，攪勻后從中隨意摸出一個球記下顏色，再把它放回盒中，不斷重復這一過程，共摸球400次，其中80次摸到黑球，你估計盒中大約有白球（　　）

  A．32個

  B．36個

  C．40個

  D．42個
  組卷：1329引用：34難度：0.9

  解析

• 4．如圖，在數軸上，點A、B分別表示a、b,且a+b=0，若|a-b|=6，則點A表示的數為（　　）

  A．-3

  B．0

  C．3

  D．-6
  組卷：486引用：10難度：0.8

  解析

• 5．在四邊形ABCD是菱形，其中AB=4cm,則四邊形ABCD的周長是（　　）

  A．5cm

  B．8cm

  C．12cm

  D．16cm
  組卷：524引用：9難度：0.8

  解析

• 6．下列命題是真命題的是（　　）

  A．對角線互相垂直平分的四邊形是正方形

  B．對角線相等的四邊形是平行四邊形

  C．對角線互相垂直的四邊形是菱形

  D．對角線互相平分且相等的四邊形是矩形
  組卷：1428引用：57難度：0.5

  解析

• 7．若

  m

  n

  =

  3

  7

  ，則

  m

  +

  n

  n

  的值為（　　）

  A． 10 7

  B． 7 10

  C． 3 7

  D． 4 7
  組卷：769引用：11難度：0.8

  解析

三、解答題（本大題共7小題，解答要求寫出文字說明、證明過程或計算步驟）

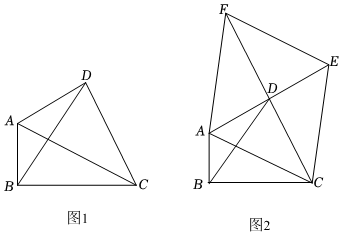• 21．定義：只有一組對角是直角的四邊形叫做損矩形，連接它的兩個非直角頂點的線段叫做這個損矩形的直徑．如圖1，∠ABC=∠ADC=90°，四邊形ABCD是損矩形，則該損矩形的直徑是線段AC．同時我們還發現損矩形中有公共邊的兩個三角形角的特點：在公共邊的同側的兩個角是相等的．如圖1中：△ABC和△ABD有公共邊AB，在AB同側有∠ADB和∠ACB，此時∠ADB=∠ACB；再比如△ABC和△BCD有公共邊BC，在CB同側有∠BAC和∠BDC，此時∠BAC=∠BDC．
  （1）請在圖1中再找出一對這樣的角來：

  =

  ；
  （2）如圖2，△ABC中，∠ABC=90°，以AC為一邊向外作菱形ACEF，D為菱形ACEF對角線的交點，連接BD．
  ①四邊形ABCD

  損矩形（填“是”或“不是”）；
  ②當BD平分∠ABC時，判斷四邊形ACEF為何種特殊的四邊形？請說明理由；
  ③若∠ACE=60°，AB=4，BD=5

  3

  ，求BC的長．
  組卷：905引用：5難度：0.3

  解析

• 22．如圖，在△ABC中，∠C=90°，AC=6cm,BC=8cm,D、E分別是AC、AB的中點，連接DE．點P從點D出發，沿DE方向勻速運動，速度為1cm/s；同時，點Q從點B出發，沿BA方向勻速運動，速度為2cm/s,當點P停止運動時，點Q也停止運動．連接PQ，設運動時間為t（0＜t＜4）s.解答下列問題：
  （1）DE=

  cm,QE=

  （用含有t的代數式表示）；
  （2）請求出t為何值時，以點E、P、Q為頂點的三角形與△ADE相似？
  （3）當t為何值時，△EPQ為等腰三角形？（直接寫出答案即可）.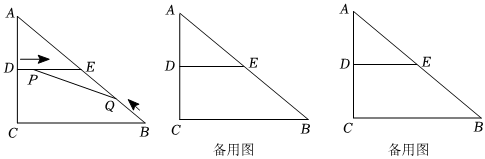
  組卷：544引用：2難度：0.1

  解析