2022-2023學年浙江省杭州市西湖高級中學高二（上）月考數學試卷（10月份）

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．直線x+

  3

  y-2=0的傾斜角為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 5 π 6
  組卷：438引用：38難度：0.8

  解析

• 2．過點A（1，2）的直線在兩坐標軸上的截距之和為零，則該直線方程為（　　）

  A．x-y+1=0	B．x+y-3=0
  C．y=2x或x+y-3=0	D．y=2x或x-y+1=0
  組卷：843引用：9難度：0.8

  解析

• 3．直線2x+3y-6=0關于點（1，1）對稱的直線方程為（　　）

  A．3x-2y+2=0

  B．2x+3y+7=0

  C．3x-2y-12=0

  D．2x+3y-4=0
  組卷：260引用：5難度：0.7

  解析

• 4．已知直線l₁：x+（m+1）y+m=0，l₂：mx+2y+1=0，則l₁∥l₂“的一個必要不充分條件是（　　）

  A．m=-2

  B．m=1

  C．m=-2或m=1

  D．m=2或m=1
  組卷：345引用：9難度：0.8

  解析

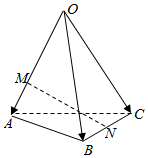• 5．如圖，空間四邊形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點M在

  OA

  上，且OM=2MA，點N為BC中點，則

  MN

  =（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  組卷：2456引用：155難度：0.9

  解析

• 6．從裝有兩個紅球和兩個黑球的口袋內任取兩個球，現有如下說法：
  ①至少有一個黑球與都是黑球是互斥而不對立的事件；
  ②至少有一個黑球與至少有一個紅球不是互斥事件；
  ③恰好有一個黑球與恰好有兩個黑球是互斥而不對立的事件；
  ④至少有一個黑球與都是紅球是對立事件．
  在上述說法中，正確的個數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：58引用：4難度：0.7

  解析

• 7．已知A（-2，0），B（4，a）兩點到直線l：3x-4y+1=0的距離相等，則a=（　　）

  A．2

  B． 9 2

  C．2或-8

  D．2或 9 2
  組卷：1482引用：25難度：0.8

  解析

四、解答題：本題共6小題，共70分．解答應寫出必要的文字說明、證明過程或演算步驟．

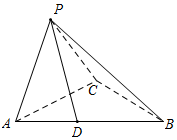• 21．如圖，在三棱錐P-ABC中，AC=2，BC=4，△PAC為正三角形，D為AB的中點，AC⊥PD，∠PCB=90°．
  （1）求證：BC⊥平面PAC；
  （2）求PD與平面PBC所成角的正弦值．
  組卷：288引用：8難度：0.6

  解析

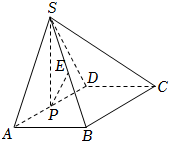• 22．如圖，在四棱錐S-ABCD中，四邊形ABCD是矩形，△SAD是正三角形，且平面SAD⊥平面ABCD，AB=1，P為棱AD的中點，四棱錐S-ABCD的體積為

  2

  3

  3

  ．
  （1）若E為棱SB的中點，求證：PE∥平面SCD；
  （2）在棱SA上是否存在點M，使得平面PMB與平面SAD所成銳二面角的余弦值為

  2

  3

  5

  ？若存在，指出點M的位置并給以證明；若不存在，請說明理由．
  組卷：290引用：24難度：0.5

  解析