2022年貴州省貴陽市修文縣高考數學二模試卷（理科）

一、單選題

• 1．已知集合A={x|x²-5x+4≤0}，B={x|2^x≤4，x∈Z}，則A∩B=（　　）

  A．[1，2]

  B．[1，4]

  C．{1，2}

  D．{1，4}
  組卷：153引用：9難度：0.8

  解析

• 2．已知i是虛數單位，則復數

  -

  1

  +

  2

  i

  2

  +

  i

  的虛部是（　　）

  A．1

  B．i

  C．-1

  D．-i
  組卷：158引用：1難度：0.8

  解析

• 3．我國運動員在第24～30屆奧運會上獲得的獎牌數量（單位：枚）統計如圖折線圖所示，則下列說法錯誤的是（　　）
  

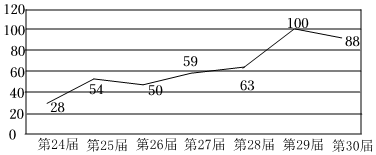
  A．從第24屆奧運會到第29屆奧運會，獲得的獎牌數量總體上呈上升趨勢

  B．相對于上一屆奧運會，第29屆奧運會獲得的獎牌數量的增長率是最高的

  C．相對于上一屆奧運會，第26屆和第30屆奧運會上獲得的獎牌數量的增長率均是負數

  D．從第24～30屆奧運會中任取一屆，獲得的獎牌數量不低于60枚的概率為 3 7
  組卷：65引用：2難度：0.9

  解析

• 4．牛頓曾經提出了常溫環境下的溫度冷卻模型：

  t

  =

  -

  1

  k

  ln

  θ

  -

  θ

  0

  θ

  1

  -

  θ

  0

  （t為時間，單位分鐘，θ₀為環境溫度，θ₁為物體初始溫度，θ為冷卻后溫度），假設一杯開水溫度θ₁=100℃，環境溫度θ₀=20℃，常數k=0.2，大約經過多少分鐘水溫降為40℃？（結果保留整數，參考數據：ln2≈0.7）（　　）

  A．9

  B．8

  C．7

  D．6
  組卷：184引用：13難度：0.7

  解析

• 5．設雙曲線D：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0），若右焦點F（5，0）到它的一條漸近線的距離為3，則該雙曲線的離心率e的值為（　　）

  A． 3 2

  B． 4 3

  C． 5 3

  D． 5 4
  組卷：154引用：5難度：0.7

  解析

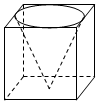• 6．如圖所示的幾何體是一個正方體挖掉一個圓錐（圓錐的底面圓與正方體的上底面正方形各邊相切，頂點在下底面上），用一個垂直于正方體某個面的平面截該幾何體，下列圖形中一定不是其截面圖的是（　　）

  A．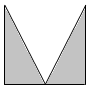

  B．

  C．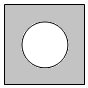

  D．
  組卷：110引用：3難度：0.8

  解析

• 7．已知等比數列{a_n}的公比為q,則“a₁＞0且q＞1”是“{a_n}為遞增數列”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：179引用：3難度：0.7

  解析

三、解答題

• 22．已知在△ABC中，角A，B，C所對的邊分別為a,b,c,且滿足asinAcosC+csinAcosA-

  3

  bcosA=0．
  （1）求角A的大小；
  （2）若△ABC的面積為4

  3

  ，且2b=a+c,求△ABC的周長．
  組卷：274引用：2難度：0.5

  解析

• 23．在極坐標系xOy中，已知曲線C₁的極坐標方程為

  ρsin

  （

  θ

  +

  π

  6

  ）

  =

  2

  ，曲線C₂的極坐標方程為ρ²（1+3sin²θ）=7．以坐標原點為極點，極軸為x軸正半軸建立直角坐標系．
  （1）求曲線C₁，C₂，的直角坐標方程；
  （2）在極坐標系中，射線

  θ

  =

  π

  3

  與曲線C₁交于點M，射線

  θ

  =

  π

  6

  與曲線C₂交于點N，求△MON的面積（其中O為坐標原點）．
  組卷：85引用：2難度：0.7

  解析