2023-2024學年廣東省深圳市南山為明學校高二(上)期中數學試卷
發布:2024/10/3 5:0:1
一、單選題(本題共8小題,每小題5分,共40分。在每小題給出的四個選項中,只有一項是符合題目要求的。)
-
1.已知直線l與x軸所成角為30°,直線l的斜率為( )
A. 33B. 3C.± 33D. ±3組卷:401引用:8難度:0.7 -
2.若直線x-2y+5=0與直線2x+my-6=0互相垂直,則實數m等于( )
A.1 B.2 C.4 D. 12組卷:165引用:5難度:0.9 -
3.圓的一條直徑的兩個端點是(2,0),(2,-2),則此圓的方程是( )
A.(x-2)2+(y-1)2=1 B.(x-2)2+(y+1)2=1 C.(x+2)2+(y-1)2=1 D.(x+2)2+(y+1)2=1 組卷:221引用:5難度:0.9 -
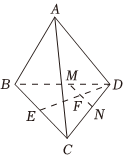 4.如圖,在空間四邊形ABCD中,E,M,N分別是邊BC,BD,CD的中點,DE,MN交于F點,則=( )12AB+12AC+EF
4.如圖,在空間四邊形ABCD中,E,M,N分別是邊BC,BD,CD的中點,DE,MN交于F點,則=( )12AB+12AC+EFA. ADB. AFC. FAD. EM組卷:72引用:4難度:0.8 -
5.設
,a1=2m-j+k,a2=m+3j-2k,a3=-2m+j-3k,其中a4=3m+2j+5k,m,j是兩兩垂直的單位向量,若k,則實數λ,μ,v的值分別是( )a4=λa1+μa2+va3A.1,-2,3 B.-2,1,-3 C.-2,1,3 D.-1,2,3 組卷:75引用:3難度:0.5 -
6.已知空間直角坐標系O-xyz中有一點A(-1,-1,2),點B是xOy平面內的直線x+y=1上的動點,則A,B兩點的最短距離是( )
A. 6B. 342C.3 D. 172組卷:183引用:20難度:0.9 -
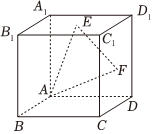 7.已知正方體ABCD-A1B1C1D1的棱長為2,E、F分別為上底面A1B1C1D1和側面CDD1C1的中心,則點A1到平面AEF的距離為( )
7.已知正方體ABCD-A1B1C1D1的棱長為2,E、F分別為上底面A1B1C1D1和側面CDD1C1的中心,則點A1到平面AEF的距離為( )A. 21111B. 1111C. 114D. 41111組卷:49引用:1難度:0.7
四、解答題(本題共6小題,共70分。解答應寫出文字說明、證明過程或演算步驟。)
-
21.已知圓C過點M(-3,2),圓心C在直線x-y+3=0上,且圓C與x軸相切.
(1)求圓C的標準方程;
(2)過點A(-3,3)作圓C的切線,求此切線的方程.組卷:236引用:4難度:0.7 -
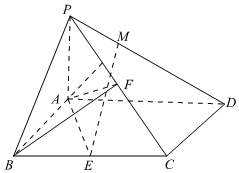 22.如圖所示,四棱錐P-ABCD中,PA⊥菱形ABCD所在的平面,∠ABC=60°,點E、F分別是BC、PC的中點,M是線段PD上的點.
22.如圖所示,四棱錐P-ABCD中,PA⊥菱形ABCD所在的平面,∠ABC=60°,點E、F分別是BC、PC的中點,M是線段PD上的點.
(1)求證:平面AEM⊥平面PAD;
(2)當AB=AP時,是否存在點M,使直線EM與平面ABF所成角的正弦值為?若存在,請求出217的值,若不存在,請說明理由.PMPD組卷:212引用:4難度:0.4


