2022-2023學年陜西省西安市鄠邑區高二（下）期中數學模擬試卷（理科）

一、選擇題（本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

• 1．已知

  z

  -

  2

  z

  =

  1

  +

  6

  i

  ，則z的虛部為（　　）

  A．-6

  B．-6i

  C．2

  D．2i
  組卷：44引用：4難度：0.8

  解析

• 2．反證法證明命題“若a∈R，則函數y=x³+ax+b至少有一個零點”時，正確的反設為（　　）

  A．若a∈R，則函數y=x3+ax+b恰好有一個零點

  B．若a∈R，則函數y=x3+ax+b至多有一個零點

  C．若a∈R，則函數y=x3+ax+b至多有兩個零點

  D．若a∈R，則函數y=x3+ax+b沒有零點
  組卷：14引用：1難度：0.7

  解析

• 3．已知函數f_i（x）的導函數為f'_i（x）（i=1，2，3），若f₁（x）、f₂（x）、f₃（x）的圖象如圖所示，則（　　）

  A．f′1（a）＞f'2（a）＞f'3（a）	B．f'1（a）＞f'3（a）＞f'2（a）
  C．f'2（a）＞f'1（a）＞f'3（a）	D．f'3（a）＞f'1（a）＞f'2（a）
  組卷：124引用：2難度：0.9

  解析

• 4．若y=f（x）是奇函數，則

  ∫

  1

  -

  1

  f

  （

  x

  ）

  dx

  =（　　）

  A．1	B．0
  C． 2 ∫ 0 - 1 f （ x ） dx	D． 2 ∫ 1 0 f （ x ） dx
  組卷：32引用：1難度：0.8

  解析

• 5．下列計算不正確的是（　　）

  A．（e-x）′=e-x	B．（ln（2x+1））'= 2 2 x + 1
  C．（cosx）'=-sinx	D． （ x ） ′ = 1 2 x
  組卷：56引用：1難度：0.8

  解析

• 6．用數學歸納法證明“2ⁿ≥n²（n∈N^*，n≥4）”時，第二步應假設（　　）

  A．當n=k（k∈N*，k≥2）時，2k≥k2成立

  B．當n=k（k∈N*，k≥3）時，2k≥k2成立

  C．當n=k（k∈N*，k≥4）時，2k≥k2成立

  D．當n=k（k∈N*，k≥5）時，2k≥k2成立
  組卷：51引用：1難度：0.8

  解析

• 7．若函數y=f（x）的導函數y=φ（x）=f'（x）圖象如圖所示，則（　　）

  A．-3是函數f（x）的極小值點

  B．-1是函數y=f（x）的極小值點

  C．函數f（x）的單調遞減區間為（-2，1）

  D．φ'（x）＜0的解集為（-∞，-3）
  組卷：157引用：6難度：0.8

  解析

三、解答題（本大題共6小題，滿分70分，解答應寫出必要的文字說明、證明過程或演算步驟．）

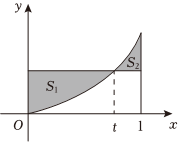• 21．如圖，在區間[0，1]上給定曲線y=x²，左邊陰影部分的面積為S₁，右邊陰影部分的面積記為S₂．
  （1）當

  t

  =

  1

  2

  時，求S₁的值；
  （2）當0≤t≤1時，求S₁+S₂的最小值．
  組卷：3引用：1難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  xlnx

  -

  1

  2

  m

  x

  2

  -

  x

  （

  m

  ∈

  R

  ）

  ．
  （1）若m=0，求函數f（x）的單調區間；
  （2）若函數f（x）在（0，+∞）上是減函數，求實數m的取值范圍．
  組卷：405引用：8難度：0.5

  解析