2022-2023學年浙江省寧波市余姚市夢麟中學高二（上）月考數學試卷（10月份）

一、單選題（每小題5分）

• 1．已知直線l過定點A（2，3，1），且

  n

  =（0，1，1）為其一個方向向量，則點P（4，3，2）到直線l的距離為（　　）

  A． 3 2 2

  B． 2 2

  C． 10 2

  D． 2
  組卷：667引用：15難度：0.8

  解析

• 2．已知平面α，β的法向量分別為

  n

  1

  =（x,1，-1），

  n

  2

  =（6，y,3），且α∥β，則x+y=（　　）

  A． 4 3

  B．1

  C．-3

  D．-5
  組卷：256引用：4難度：0.8

  解析

• 3．在平行六面體ABCD-A₁B₁C₁D₁中，E為C₁D₁的中點，F為BB₁的中點，

  AE

  =

  a

  ，

  AF

  =

  b

  ，

  AD

  =

  c

  ，則

  A

  A

  1

  =（　　）

  A． 4 3 a - 3 2 b - c	B． 4 3 a - b - 4 3 c
  C． 4 3 a - 2 3 b - 4 3 c	D． a - 3 2 b - 4 3 c
  組卷：475引用：9難度：0.5

  解析

• 4．已知O為坐標原點，向量

  a

  =（-2，1，1），點A（-3，-1，4），B（-2，-2，2）．若點E在直線AB上，且

  OE

  ⊥

  a

  ，則點E的坐標為（　　）

  A．（- 6 5 ，- 14 5 ， 2 5 ）	B．（ 6 5 ， 14 5 ，- 2 5 ）
  C．（ 6 5 ，- 14 5 ， 2 5 ）	D．（- 6 5 ， 14 5 ，- 2 5 ）
  組卷：143引用：6難度：0.7

  解析

• 5．直線l₁：ax-y+b=0，l₂：bx+y-a=0（ab≠0，a、b∈R）的圖象可能是（　　）

  A．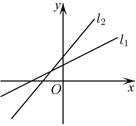

  B．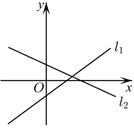

  C．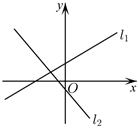

  D．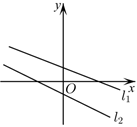
  組卷：94引用：9難度：0.7

  解析

• 6．關于空間向量，以下說法不正確的是（　　）

  A．若兩個不同平面α，β的法向量分別是 u ， ν ，且 u = （ 1 ， 2 ，- 2 ） ， ν = （ 2 ， 1 ， 2 ） ，則α⊥β

  B．若直線l的方向向量為 e = （ 1 ， 0 ， 3 ） ，平面α的法向量為 n = （ - 2 ， 0 ， 2 3 ） ，則直線l∥α

  C．若對空間中任意一點O，有 OP = 1 4 OA + 1 4 OB + 1 2 OC ，則P，A，B，C四點共面

  D．兩個非零向量與任何一個向量都不能構成空間的一個基底，則這兩個向量共線
  組卷：265引用：9難度：0.7

  解析

• 7．已知點M（-1，0），N（1，0），若直線上存在點P，使得

  PM

  ?

  PN

  =

  0

  ，則稱該直線為“相關點直線”．給出下列直線：①y=x+3；

  ②

  y

  =

  4

  3

  x

  ； ③y=2； ④y=2x+1，其中為“相關點直線”的是（　　）

  A．①③

  B．②④

  C．②③

  D．③④
  組卷：22引用：2難度：0.7

  解析

四、解答題（共70分，解答應寫出文字說明、證明過程或演算步驟）

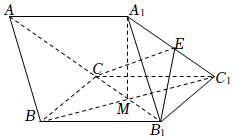• 21．在三棱柱ABC-A₁B₁C₁中，側面正方形BB₁C₁C的中心為點M，A₁M⊥平面BB₁C₁C，且

  B

  B

  1

  =

  2

  ，

  AB

  =

  3

  ，點E滿足

  A

  1

  E

  =

  λ

  A

  1

  C

  1

  （

  0

  ≤

  λ

  ≤

  1

  ）

  ．
  （1）若A₁B∥平面B₁CE，求λ的值；
  （2）求點E到平面ABC的距離；
  （3）若平面ABC與平面B₁CE所成角的正弦值為

  2

  5

  5

  ，求λ的值．
  組卷：162引用：4難度：0.4

  解析

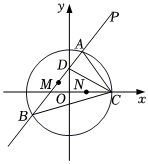• 22．如圖，在平面直角坐標系xOy中，已知點P（2，4），圓O：x²+y²=4與x軸的正半軸的交點是Q，過點P的直線l與圓O交于不同的兩點A，B．
  （1）若直線l與y軸交于D，且

  DP

  ?

  DQ

  =16，求直線l的方程；
  （2）設直線QA，QB的斜率分別是k₁，k₂，求k₁+k₂的值；
  （3）設AB的中點為M，點N（

  4

  3

  ，0），若MN=

  13

  3

  OM，求△QAB的面積．
  組卷：526引用：5難度：0.3

  解析