2023年陜西省咸陽市秦都區電建學校中考數學一模試卷

一、選擇題（共8小題，每小題3分，計24分.每小題只有一個選項是符合題意的）

• 1．實數-

  2

  9

  的倒數是（　　）

  A．- 9 2

  B．- 2 9

  C． 2 9

  D． 9 2
  組卷：98引用：2難度：0.8

  解析

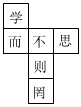• 2．“學而不思則罔，思而不學則殆”體現了學習和思考的重要性．如圖是每個面上都有一個漢字的正方體的一種表面展開圖，那么在原正方體中與“而”字相對面上的字是（　　）

  A．不

  B．思

  C．則

  D．罔
  組卷：66引用：1難度：0.8

  解析

• 3．計算（-4ab²）²?b?²的結果正確的是（　　）

  A．-4a2b2

  B．4a2b?

  C．-16a2b2

  D．16a2b2
  組卷：174引用：1難度：0.9

  解析

• 4．如圖，將一副三角尺按圖中所示位置擺放，點C在FD的延長線上，點C、F分別為直角頂點，且∠A=60°，∠E=45°，若AB∥CF，則∠CBD的度數是（　　）

  A．15°

  B．20°

  C．25°

  D．30°
  組卷：1201引用：16難度：0.7

  解析

• 5．如圖，在矩形ABCD中，連接AC，點E是BC上一點，連接AE，若S_△ABE=9，AB=6，CE=5，則sin∠ACD的值為（　　）

  A． 3 5

  B． 3 4

  C． 4 5

  D． 2 3
  組卷：93引用：1難度：0.5

  解析

• 6．在平面直角坐標系中，將直線y=2x+6向右平移m個單位長度后得到的直線與直線y=-x+4的交點在第一象限，則m的取值范圍是（　　）

  A．1＜m＜7

  B．1＜m

  C．m＞7

  D．m＜1
  組卷：142引用：1難度：0.9

  解析

• 7．如圖，AB是⊙O的直徑，點C、D是⊙O上的兩點，連接AC、OC、OD、CD，且AC∥OD，若AB=6，∠ACD=15°，則AC的長為（　　）

  A． 2 3

  B．4

  C． 3 2

  D． 3 3
  組卷：178引用：2難度：0.6

  解析

• 8．二次函數y=-x²-6x+c（c＞0）的圖象上有兩點A（x₁，y₁），B（x₂，y₂）．若-5＜x₁＜-3＜0＜x₂，則y₁與y₂的大小關系是（　　）

  A．y1＜y2	B．y1＞y2
  C．y1=y2	D．y1與y2的大小不確定
  組卷：182引用：1難度：0.5

  解析

三、解答題（共13小題，計81分.解答應寫出過程）

• 25．如圖，拋物線y=ax²+bx+6與x軸交于A（2，0），B（-6，0）兩點．
  （1）求該拋物線的表達式；
  （2）點P是拋物線上一點，點Q是拋物線對稱軸上一點，是否存在點P，使得以B、Q、C、P為頂點的四邊形是平行四邊形，若存在，請求出點P的坐標；若不存在，請說明理由．
  組卷：265引用：1難度：0.2

  解析

• 26．【問題提出】
  （1）如圖1，點A、B在直線l的同側，點A到直線l的距離AC=2，點B到直線l的距離BD=4，A、B兩點的水平距離CD=8，點P是直線l上的一個動點，則AP+BP的最小值是

  ；
  【問題探究】
  （2）如圖2，在矩形ABCD中，AB=4，BC=2，G是AD的中點，線段EF在邊AB上左右滑動，若EF=1，求GE+CF的最小值；
  【問題解決】
  （3）如圖3，某公園有一塊形狀為四邊形ABCD的空地，管理人員規劃修兩條小路AC和BD（小路的寬度忽略不計，兩條小路交于點P），并在AD和BC上分別選取點M、N，沿PM、PN和MN修建地下水管，為了節約成本，要使得線段PM、PN與MN之和最小．
  已測出∠ACB=45°，∠ADB=60°，∠CPD=75°，PC=50

  2

  m,PD=40m,管理人員的想法能否實現，若能，請求出PM+PN+MN的最小值，若不能，請說明理由．
  
  組卷：385引用：2難度：0.2

  解析