2022-2023學(xué)年重慶市九龍坡區(qū)鐵路中學(xué)高二（上）期中數(shù)學(xué)試卷

一、單項(xiàng)選擇（本大題共8小題.每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.）

• 1．已知

  a

  =

  （

  -

  2

  ，

  1

  ，

  3

  ）

  ，

  b

  =

  （

  -

  1

  ，

  2

  ，

  1

  ）

  ，則

  a

  ?

  b

  =（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：52引用：3難度：0.8

  解析

• 2．已知橢圓

  x

  2

  m

  +

  y

  2

  3

  =

  1

  的一個(gè)焦點(diǎn)坐標(biāo)為（-1，0），則m的值為（　　）

  A．2

  B．4

  C．5

  D．6
  組卷：147引用：6難度：0.7

  解析

• 3．圓x²+y²-2x=0與圓x²+y²+4y=0的公共弦長(zhǎng)等于（　　）

  A． 3

  B． 4 3 3

  C． 2 5 5

  D． 4 5 5
  組卷：80引用：2難度：0.6

  解析

• 4．在正方體ABCD-A₁B₁C₁D₁中，O為面AA₁B₁B的中心，O₁為面A₁B₁C₁D₁的中心，若E為CD的中點(diǎn)，則異面直線AE與OO₁所成角的余弦值為（　　）

  A． 2 5 5

  B． 10 5

  C． 5 10

  D． 5 5
  組卷：63引用：5難度：0.7

  解析

• 5．設(shè)實(shí)數(shù)x,y滿足x+y=4，則

  x

  2

  +

  y

  2

  -

  2

  x

  +

  2

  y

  +

  2

  的最小值為（　　）

  A． 2

  B．4

  C． 2 2

  D．8
  組卷：214引用：4難度：0.7

  解析

• 6．若直線（2m²+m-3）x+（m²-m）y=4m-1與直線2x-3y-5=0平行，則實(shí)數(shù)m的值為（　　）

  A．- 9 8

  B．1

  C．1或- 9 8

  D．-1
  組卷：31引用：3難度：0.9

  解析

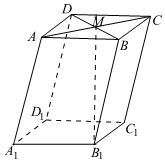• 7．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，M為AC與BD的交點(diǎn)，若|

  A

  1

  B

  1

  |=|

  A

  1

  D

  1

  |=|

  A

  1

  A

  |=2，∠AA₁D₁=90°，∠AA₁B₁=∠B₁A₁D₁=60°，則|

  B

  1

  M

  |的值為（　　）

  A．1

  B． 3

  C．2

  D． 2 3
  組卷：155引用：7難度：0.5

  解析

四、解答題（本大題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.）

• 21．公元前3世紀(jì)，古希臘數(shù)學(xué)家阿波羅尼斯在《平面軌跡》一書中，曾研究了眾多的平面軌跡問題，其中有如下結(jié)果：平面內(nèi)到兩定點(diǎn)距離之比等于已知數(shù)的動(dòng)點(diǎn)軌跡為直線或圓，后世把這種圓稱之為阿波羅尼斯圓．已知平面直角坐標(biāo)系中A（-2，0），B（1，0）且|PA|=2|PB|．
  （1）求點(diǎn)P的軌跡方程；
  （2）若點(diǎn)P在（1）的軌跡上運(yùn)動(dòng)，點(diǎn)M為AP的中點(diǎn)，求點(diǎn)M的軌跡方程；
  （3）若點(diǎn)P（x,y）在（1）的軌跡上運(yùn)動(dòng)，求

  t

  =

  y

  +

  4

  x

  -

  6

  的取值范圍．
  組卷：81引用：7難度：0.5

  解析

• 22．已知正方形的邊長(zhǎng)為4，E，F(xiàn)分別為AD，BC的中點(diǎn)，以EF為棱將正方形ABCD折成如圖所示的60°的二面角，點(diǎn)M在線段AB上．
  
  （1）若M為AB的中點(diǎn)，且直線MF與由A，D，E三點(diǎn)所確定平面的交點(diǎn)為O，試確定點(diǎn)O的位置，并證明直線OD∥平面EMC；
  （2）是否存在點(diǎn)M，使得直線DE與平面EMC所成的角為60°；若存在，求此時(shí)平面MEC與平面ECF的夾角的余弦值，若不存在，說明理由．
  組卷：210引用：3難度：0.4

  解析