2023-2024學(xué)年湖南省株洲二中教育集團高三（上）開學(xué)聯(lián)考數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x²≤1}，B={x|x²-2x-3＜0}，則A∩B=（　　）

  A．（-1，1]

  B．[-1，1]

  C．（-1，3）

  D．[-1，3）
  組卷：113引用：3難度：0.9

  解析

• 2．若復(fù)數(shù)z滿足z（2-i）=1+4i（i是虛數(shù)單位），則復(fù)數(shù)z的共軛復(fù)數(shù)為（　　）

  A．- 2 5 + 9 5 i

  B．- 2 5 - 9 5 i

  C． 2 5 + 9 5 i

  D． 2 5 - 9 5 i
  組卷：698引用：4難度：0.9

  解析

• 3．已知平面向量

  a

  =

  （

  3

  ，

  1

  ）

  ，

  |

  b

  |

  =

  1

  ，

  a

  ，

  b

  的夾角為60°，

  |

  a

  +

  t

  b

  |

  =

  3

  （

  t

  ∈

  R

  ）

  ，則實數(shù)t=（　　）

  A．±1

  B．1

  C．-1

  D． 1 2
  組卷：39引用：4難度：0.7

  解析

• 4．已知正實數(shù)m,n,滿足m+n=1，則下列不等式中錯誤的是（　　）

  A． mn ≤ 1 4

  B．2m2+2n2≥1

  C． 1 m + 2 n ≥ 3 + 2 2

  D． m + n ≤ 1
  組卷：387引用：3難度：0.5

  解析

• 5．已知等差數(shù)列{a_n}的公差為d,數(shù)列{b_n}滿足

  a

  n

  ?

  b

  n

  =

  1

  （

  n

  ∈

  N

  *

  ）

  ，則“d＞0”是“{b_n}為遞減數(shù)列”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：317引用：6難度：0.7

  解析

• 6．已知函數(shù)

  f

  （

  x

  ）

  =

  lo

  g

  1

  3

  （

  3

  x

  2

  -

  ax

  +

  8

  ）

  在[-1，+∞）上單調(diào)遞減，則實數(shù)a的取值范圍是（　　）

  A．（-∞，-6]

  B．[-11，-6]

  C．（-11，-6]

  D．（-11，+∞）
  組卷：235引用：7難度：0.6

  解析

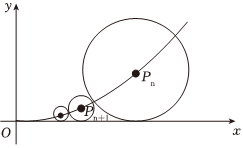• 7．如圖，在xOy平面上有一系列點P₁（x₁，y₁），P₂（x₂，y₂），…，P_n（x_n，y_n）…，對每個正整數(shù)n,點P_n位于函數(shù)y=x²（x≥0）的圖像上，以點P_n為圓心的⊙P_n都與x軸相切，且⊙P_n與⊙P_n+1外切．若x₁=1，且x_n+1＜x_n（n∈N*），T_n=x_nx_n+1，{T_n}的前n項之和為S_n，則S₂₀=（　　）

  A． 39 40

  B． 40 41

  C． 80 41

  D． 20 41
  組卷：56引用：3難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

• 21．已知F是橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左焦點，O為坐標(biāo)原點，M為橢圓上任意一點，橢圓的離心率為

  3

  2

  ，△MOF的面積的最大值為

  3

  2

  ．
  （1）求橢圓C的方程；
  （2）A，B為橢圓的左，右頂點，點P（1，0），當(dāng)M不與A，B重合時，射線MP交橢圓C于點N，直線AM，BN交于點T，求∠ATB的最大值．
  組卷：153引用：5難度：0.5

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  e

  x

  -

  1

  2

  x

  2

  -

  x

  -

  1

  ，
  （1）證明：當(dāng)x＞0時，f（x）＞0恒成立；
  （2）若關(guān)于x的方程

  f

  （

  x

  ）

  x

  +

  x

  2

  =

  asinx

  在（0，π）內(nèi)有解，求實數(shù)a的取值范圍．
  組卷：36引用：3難度：0.3

  解析