當(dāng)前位置：試卷中心 > 試卷詳情

2020-2021學(xué)年江蘇省鎮(zhèn)江市丹陽高級中學(xué)1-16班，20班高一（下）大練數(shù)學(xué)試卷（5月份）

發(fā)布：2024/4/20 14:35:0

一、單選題：本小題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．若向量
BA
=（5，6），
CA
=（2，3），則
BC
=（　　）
A．（-3，-3） B．（7，9） C．（3，3） D．（-6，-10）
組卷：384引用：5難度：0.9
解析
2．已知復(fù)數(shù)z₁=
2
（cos
π
12
+isin
π
12
），z₂=
3
（cos
π
6
+isin
π
6
），則z₁z₂的代數(shù)形式是（　　）
A．
6
（cos
π
4
+isin
π
4
） B．
6
（cos
π
12
+isin
π
12
）
C．
3
-
3
i D．
3
+
3
i
組卷：57引用：3難度：0.7
解析
3．已知
sin
（
α
+
π
6
）
=
-
1
3
，則
cos
（
2
α
+
π
3
）
=（　　）
A．
-
7
9
B．
-
4
3
9
C．
4
3
9
D．
7
9
組卷：539引用：11難度：0.8
解析
4．已知
a
與
b
滿足|
a
|=1，|
b
|=2，|
a
-2
b
|=
13
，則
a
與
b
的夾角為（　　）
A．120° B．90° C．60° D．30°
組卷：253引用：2難度：0.8
解析
5．m,n,l是三條不同的直線，α，β是兩個不同的平面，則下列判斷正確的是（　　）
A．若α⊥β，α∩β=m,m⊥n,則n⊥β
B．若m∥α，n?α，則m∥n
C．若m,n,l兩兩相交，且交于同一點，則m,n,l共面
D．若m⊥α，n⊥β，m∥n,則α∥β
組卷：50引用：2難度：0.9
解析
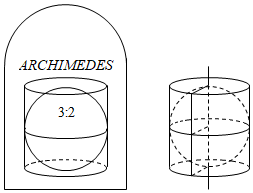6．阿基米德（Archimedes,公元前287年-公元前212年）是古希臘偉大的數(shù)學(xué)家、物理學(xué)家和天文學(xué)家．他推導(dǎo)出的結(jié)論“圓柱內(nèi)切球體的體積是圓柱體積的三分之二，并且球的表面積也是圓柱表面積的三分之二”是其畢生最滿意的數(shù)學(xué)發(fā)現(xiàn)，后人按照他生前的要求，在他的墓碑上刻著一個圓柱容器里放了一個球（如圖所示），該球與圓柱的兩個底面及側(cè)面均相切，圓柱的底面直徑與高都等于球的直徑，若球的體積為36π，則圓柱的體積為（　　）
A．36π B．45π C．54π D．63π
組卷：161引用：7難度：0.7
解析
7．在△ABC中，由角A，B，C所對的邊分別為a,b,c,且c=2（acosB-bcosA），則tan（A-B）的最大值為（　　）
A．
3
2
B．
3
C．1 D．
3
3
組卷：315引用：2難度：0.6
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題：本小題共6小題，共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟．

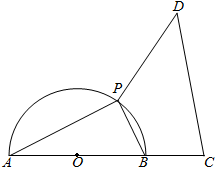21．一經(jīng)濟作物示范園的平面圖如圖所示，半圓O的直徑AB=2，點C在AB的延長線上，BC=1，點P為半圓上異于A、B兩點的一個動點，以點P為直角頂點作等腰直角△PCD，且點D與圓心O分布在PC的兩側(cè)，設(shè)∠PAC=θ．
（1）把線段PA，PC的長表示為θ的函數(shù)；
（2）現(xiàn)要在△APC和△PCD內(nèi)分別種植甲、乙兩種經(jīng)濟作物．這兩種作物單位面積的收益比為4：3，求θ為何值時，收益最大？
組卷：46引用：5難度：0.5
解析
22．已知向量
a
=（cos
3
x
2
，sin
3
x
2
），
b
=（cos
x
2
，-sin
x
2
），函數(shù)f（x）=
a
?
b
-m|
a
+
b
|+1，x∈[-
π
6
，
π
4
]，x∈R．
（1）若|
a
+
b
|=
3
，求實數(shù)x的值；
（2）若f（x）的最小值為-1，求實數(shù)m的值；
（3）是否存在實數(shù)m,使函數(shù)
g
（
x
）
=
f
（
x
）
+
24
49
m
2
，
x
∈
[
-
π
6
，
π
4
]
有四個不同的零點？若存在，求出m的取值范圍；若不存在，請說明理由．
組卷：269引用：3難度：0.2
解析