2023-2024學年遼寧省六校協作體高一（上）期中數學試卷

一、單項選擇題（本題共8小題，每小題5分，共40分）

• 1．已知集合A={x∈N^*|-3≤x≤3}，B={x|0≤x＜4}，則A∩B=（　　）

  A．{0，1，2，3}

  B．（0，3]

  C．{-1，1，2，3}

  D．{1，2，3}
  組卷：22引用：1難度：0.7

  解析

• 2．“|x-2|≠1”是“x≠3”的（　　）

  A．必要不充分條件	B．充分不必要條件
  C．充要條件	D．既不充分也不必要條件
  組卷：97引用：1難度：0.5

  解析

• 3．某服裝加工廠為了適應市場需求，引進某種新設備，以提高生產效率和降低生產成本已知購買m臺設備的總成本為

  f

  （

  m

  ）

  =

  1

  200

  m

  2

  +

  m

  +

  200

  （單位：萬元）．若要使每臺設備的平均成本最低，則應購買設備（　　）

  A．100臺

  B．200臺

  C．300臺

  D．400臺
  組卷：61引用：5難度：0.8

  解析

• 4．已知f（x²-1）的定義域為[1，3]，則f（2x-2）的定義域為（　　）

  A．[0，4]

  B．[-2，14]

  C．（-2，14）

  D．[1，5]
  組卷：166引用：1難度：0.7

  解析

• 5．函數

  f

  （

  x

  ）

  =

  x

  2

  2

  x

  -

  2

  -

  x

  的部分圖像大致為（　　）

  A．

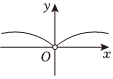
  B．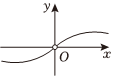

  C．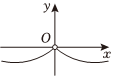

  D．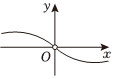
  組卷：154引用：8難度：0.8

  解析

• 6．已知定義在R上的奇函數f（x）在（-∞，0）上單調遞減，且f（2）=0，則滿足xf（x）＜0的x的取值范圍是（　　）

  A．（-∞，-2）∪（2，+∞）	B．（0，2）∪（2，+∞）
  C．（-2，0）∪（2，+∞）	D．（-∞，-2）∪（0，2）
  組卷：158引用：6難度：0.7

  解析

• 7．已知關于x的不等式ax²-bx+1＞0的解集為

  （

  -

  ∞

  ，

  2

  m

  ）

  ∪

  （

  m

  ,

  +

  ∞

  ）

  ，其中m＞0，則

  b

  +

  1

  m

  的最小值為（　　）

  A．4

  B． 2 2

  C．2

  D．1
  組卷：181引用：6難度：0.7

  解析

四、解答題（本題共6小題，共70分）

• 21．已知f（x）=3^x-3^-x．
  （1）判斷函數y=f（x）的奇偶性；
  （2）判斷函數單調性（不必證明）；
  （3）若不等式f（4^x-2^x+1+2）+f（2m+1）≤0對一切x∈[-2，2]恒成立，求實數m的取值范圍．
  組卷：63引用：4難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  x

  2

  +

  1

  ax

  +

  b

  是定義域上的奇函數，且f（-1）=-2．
  （1）求函數f（x）的解析式，判斷函數f（x）在（0，+∞）上的單調性并證明；
  （2）令g（x）=f（x）-m,若函數g（x）在（0，+∞）上有兩個零點，求實數m的取值范圍；
  （3）令

  h

  （

  x

  ）

  =

  x

  2

  +

  1

  x

  2

  -

  2

  tf

  （

  x

  ）

  （

  t

  ＜

  0

  ）

  ，若對?x₁，

  x

  2

  ∈

  [

  1

  2

  ，

  2

  ]

  都有

  |

  h

  （

  x

  1

  ）

  -

  h

  （

  x

  2

  ）

  |

  ≤

  15

  4

  ，求實數t的取值范圍．
  組卷：191引用：4難度：0.5

  解析