2020-2021學年福建省廈門市思明區湖濱中學高二（下）期中數學試卷

一、單選題

• 1．已知i為虛數單位，復數z滿足z（1+i）=1，則z的共軛復數

  z

  =（　　）

  A． 1 2 + 1 2 i

  B． 1 2 - 1 2 i

  C． - 1 2 + 1 2 i

  D． - 1 2 - 1 2 i
  組卷：10引用：4難度：0.9

  解析

• 2．已知向量

  a

  =

  （

  2

  ，-

  1

  ，

  2

  ）

  ，A（-1，x,1），B（1，-1，1），若

  a

  ⊥

  AB

  ，則實數x的值為（　　）

  A．-5

  B．0

  C．-1

  D．5
  組卷：7引用：1難度：0.7

  解析

• 3．如圖所示，已知ABCD-A₁B₁C₁D₁是平行六面體．設AC∩BD=M，N是BC₁上靠近點C₁的四等分點，若

  MN

  =

  x

  AB

  +

  y

  AD

  +

  z

  A

  A

  1

  ，則x,y,z的值為（　　）

  A． x = 1 2 ， y = 1 4 ， z = 3 4	B． x = 1 4 ， y = 1 2 ， z = 3 4
  C． x = 1 2 ， y = 3 4 ， z = 1 4	D． x = 3 4 ， y = 1 2 ， z = 1 4
  組卷：24引用：1難度：0.7

  解析

• 4．當x∈（0，5）時，函數y=xlnx的單調性（　　）

  A．是單調增函數

  B．是單調減函數

  C．在（0， 1 e ）上單調遞減，在（ 1 e ，5）上單調遞增

  D．在（0， 1 e ）上單調遞增，在（ 1 e ，5）上單調遞減
  組卷：91引用：2難度：0.9

  解析

• 5．已知f（x）在R上是可導函數，f（x）的圖象如圖所示，則不等式f′（x）＞0的解集為（　　）

  A．（-2，0）∪（2，+∞）	B．（-∞，2）∪（2，+∞）
  C．（-∞，-1）∪（1，+∞）	D．（-2，-1）∪（1，2）
  組卷：201引用：3難度：0.9

  解析

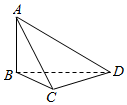• 6．在我國古代數學名著《九章算術》中，將四個面都為直角三角形的四面體稱為鱉臑，如圖，在鱉臑ABCD中，AB⊥平面BCD，且AB=BC=CD，則異面直線AC與BD所成角的余弦值為（　　）

  A． 1 2

  B．- 1 2

  C． 3 2

  D．- 3 2
  組卷：557引用：20難度：0.7

  解析

• 7．若f（x）=x³+ax²+bx-a²-7a在x=1處取得極大值10，則

  b

  a

  的值為（　　）

  A． - 3 2 或 - 1 2

  B． - 3 2 或 1 2

  C． - 3 2

  D． - 1 2
  組卷：281引用：18難度：0.7

  解析

四、解答題

• 21．如圖1，在邊長為2的菱形ABCD中，∠BAD=60°，DE⊥AB于點E，將△ADE沿DE折起到△A₁DE的位置，使A₁D⊥BE，如圖2．
  
  （1）求證：A₁E⊥平面BCDE；
  （2）在線段BD上是否存在點P，使平面A₁EP⊥平面A₁BD？若存在，求

  BP

  BD

  的值；若不存在，說明理由．
  組卷：203引用：4難度：0.4

  解析

• 22．設函數f（x）=

  x

  2

  2

  -alnx,g（x）=（1-a）x.
  （1）當a=

  1

  2

  ，x＞1時，求證：f（x）＞g（x）；
  （2）若?x∈[1，e]，使得不等式f（x）+g（x）≤a成立，求實數a的取值范圍．
  組卷：60引用：3難度：0.4

  解析