2023-2024學(xué)年安徽省皖江名校聯(lián)盟高三（上）段考數(shù)學(xué)試卷（10月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若集合A={x||x|＜3}，

  B

  =

  {

  x

  |

  4

  x

  ≥

  1

  16

  }

  ，則A∪B=（　　）

  A．[-2，3）

  B．（-3，3）

  C．[-2，+∞）

  D．（-3，+∞）
  組卷：10引用：2難度：0.8

  解析

• 2．sin2010°的值等于（　　）

  A． 1 2

  B． 3 2

  C．- 1 2

  D．- 3 2
  組卷：36引用：4難度：0.9

  解析

• 3．已知向量

  a

  =

  （

  x

  ,

  3

  ）

  ，

  b

  =

  （

  12

  ，

  x

  -

  5

  ）

  ，若向量

  a

  ，

  b

  的夾角為鈍角，則實數(shù)x的范圍是（　　）

  A．（-∞，1）	B．（1，+∞）
  C．（-∞，-4）∪（-4，1）	D．（1，9）∪（9，+∞）
  組卷：90引用：2難度：0.8

  解析

• 4．已知函數(shù)f（x）=log₂（x²-ax+3a）在區(qū)間[2，+∞）上遞增，則實數(shù)a的取值范圍是（　　）

  A．（-∞，4）

  B．（-4，4）

  C．（-4，4]

  D．[-4，+∞）
  組卷：1380引用：11難度：0.5

  解析

• 5．在△ABC中，“△ABC是銳角三角形”是“sinA+sinB+sinC＞cosA+cosB+cosC”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：180引用：2難度：0.6

  解析

• 6．若函數(shù)

  f

  （

  x

  ）

  =

  1

  2

  x

  +

  a

  +

  b

  為定義在R上的奇函數(shù)，則實數(shù)b=（　　）

  A． 1 2

  B． - 1 2

  C．1

  D．-1
  組卷：476引用：3難度：0.8

  解析

• 7．已知a=log₇6，b=log₈7，c=log₉8，則（　　）

  A．a(chǎn)＜b＜c

  B．a(chǎn)＜c＜b

  C．b＜a＜c

  D．c＜b＜a
  組卷：123引用：2難度：0.5

  解析

四、解答題：本大題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

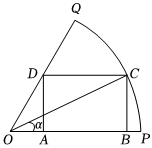• 21．如圖，已知OPQ是半徑為1，圓心角為

  θ

  （

  π

  4

  ＜

  θ

  ＜

  π

  2

  ）

  的扇形，C是扇形弧上的動點，ABCD是扇形的內(nèi)接矩形，設(shè)∠POC=α（0＜α＜θ）．
  （1）若

  θ

  =

  5

  π

  12

  ，

  α

  =

  π

  4

  ，求線段OA的長；
  （2）已知當(dāng)

  α

  =

  π

  6

  時，矩形ABCD的面積S最大．求圓心角θ的大小，并求此時矩形ABCD面積S的最大值是多少？
  組卷：83引用：1難度：0.7

  解析

• 22．已知函數(shù)f（x）=e^x-1+a,函數(shù)g（x）=ax+lnx,a∈R．令函數(shù)h（x）=f（x）-g（x）．
  （1）若曲線y=f（x）與直線y=x相切，
  ①求實數(shù)a的值；
  ②證明：h（x）≥1；
  （2）若函數(shù)h（x）有且僅有一個零點x₀，證明：x₀＜2．
  組卷：22引用：2難度：0.5

  解析