2022-2023學(xué)年陜西省西安市鐵一中學(xué)高二（下）月考數(shù)學(xué)試卷（文科）（三）

一、選擇題（本大題共12個(gè)小題，每小題5分，共計(jì)60分，在每小題給出的四個(gè)選項(xiàng)中只有一項(xiàng)是符合題目要求的）

• 1．已知集合A={x∈N||x-1|≤2}，B={2，3，4}，則A∪B=（　　）

  A．{-1，0，1，2，3，4}	B．{0，1，2，3，4}
  C．{2，3}	D．{1，2，3，4}
  組卷：87引用：3難度：0.7

  解析

• 2．設(shè)z=

  2

  +

  i

  1

  +

  i

  2

  +

  i

  5

  ，則

  z

  =（　　）

  A．1-2i

  B．1+2i

  C．2-i

  D．2+i
  組卷：2967引用：10難度：0.7

  解析

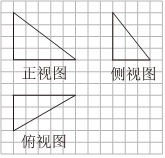• 3．如圖是某三棱錐的三視圖，已知網(wǎng)格紙的小正方形邊長(zhǎng)是1，則這個(gè)三棱錐中最長(zhǎng)棱的長(zhǎng)為（　　）

  A．5

  B． 34

  C． 41

  D．7
  組卷：112引用：6難度：0.7

  解析

• 4．給出下列四個(gè)選項(xiàng)中，其中正確的選項(xiàng)有（　　）

  A．“1＜m＜7”是方程“ x 2 m - 1 + y 2 7 - m = 1 表示橢圓的充要條件”

  B．已知a表示直線，α，β表示兩個(gè)不同的平面，若a?α，a∥β，則α∥β

  C．命題“?x∈R，使得x2+x-1＜0”的否定是：“?x∈R，均有x2+x-1＞0”

  D．函數(shù)y=loga（x-1）+1（a＞0且a≠1）的圖像必過（2，1）
  組卷：5引用：4難度：0.8

  解析

• 5．已知向量

  a

  =（3，2），

  b

  =（x,y），且實(shí)數(shù)x,y滿足約束條件

  x - 2 y - 2 ≤ 0

  x - y + 1 ≥ 0

  y ≤ 0

  ，則z=

  a

  ?

  b

  的最大值為（　　）

  A．-18

  B．-10

  C．-2

  D．6
  組卷：144引用：2難度：0.5

  解析

• 6．已知f（x）的圖象如圖，則f（x）的解析式可能是（　　）

  A． f （ x ） = cos （ πx ） 2 （ e x + e - x ）

  B． f （ x ） = cos （ πx ） 2 （ e x - e - x ）

  C． f （ x ） = （ e x - e - x ） cos （ πx ） 2

  D． f （ x ） = （ e x + e - x ） sin （ πx ） 2
  組卷：34引用：4難度：0.7

  解析

• 7．已知函數(shù)

  f

  （

  x

  ）

  =

  x

  3

  -

  3

  2

  x

  2

  -

  alnx

  （

  a

  ∈

  R

  ）

  在（0，+∞）上單調(diào)遞增，則a的取值范圍是（　　）

  A． a ＜ 2 3

  B． a ≤ 2 3

  C． a ＜ - 4 9

  D． a ≤ - 4 9
  組卷：73引用：3難度：0.5

  解析

三、解答題（本大題共6小題，共70分.解答應(yīng)寫出文字說明，證明過程或演算步驟.）

• 21．已知等軸雙曲線C的焦點(diǎn)在x軸上，焦距為

  4

  2

  ．
  （1）求雙曲線的標(biāo)準(zhǔn)方程；
  （2）斜率為k的直線l過點(diǎn)P（1，0），且直線l與雙曲線C的兩支分別交于A、B兩點(diǎn)，
  ①求k的取值范圍；
  ②若D是B關(guān)于x軸的對(duì)稱點(diǎn)，證明直線AD過定點(diǎn)，并求出該定點(diǎn)坐標(biāo)．
  組卷：127引用：3難度：0.6

  解析

• 22．已知函數(shù)f（x）=lnx+x²-ax,（a∈R）．
  （1）若對(duì)任意的x∈（0，+∞），都有f（x）≤x²恒成立，求實(shí)數(shù)a的取值范圍；
  （2）設(shè)f（x）存在兩個(gè)極值點(diǎn)x₁，x₂且x₁＜x₂．若

  0

  ＜

  x

  1

  ＜

  1

  2

  ，證明：

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  ＞

  3

  4

  -

  ln

  2

  ．
  組卷：68引用：3難度：0.4

  解析