2023年福建省高考數學測評試卷（4月份）

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知全集I={x|x∈N^*，x²＜80}，A={1，3，4，7}，B={4，5，6，7}，則?_I（A∪B）=（　　）

  A．{2，5，6}	B．{1，2，3，8}
  C．{2，8}	D．{1，3，4，5，6，7}
  組卷：29引用：3難度：0.7

  解析

• 2．若復數

  z

  =

  a

  -

  2

  i

  2

  +

  i

  （

  a

  ∈

  R

  ）

  ，

  |

  z

  |

  =

  2

  2

  ，

  z

  在復平面上對應的點在第四象限，則a=（　　）

  A．6

  B．4

  C．-4

  D．-6
  組卷：42引用：2難度：0.8

  解析

• 3．已知等差數列{a_n}的前n項和為S_n，S₁₀+a₂₂=11，則S₁₃=（　　）

  A．11

  B．12

  C．13

  D．14
  組卷：179引用：3難度：0.8

  解析

• 4．已知p：?x∈[1，5]，x²-4x+a-2＞0恒成立，則p的一個充分不必要條件是（　　）

  A．a＞1

  B．a2＞36

  C．2a＞64

  D．log2a＞3
  組卷：70引用：3難度：0.7

  解析

• 5．函數

  f

  （

  x

  ）

  =

  e

  x

  -

  e

  -

  x

  -

  1

  x

  的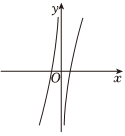圖像大致是（　　）

  A．

  B．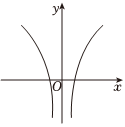

  C．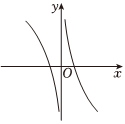

  D．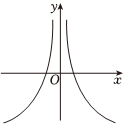
  組卷：65引用：3難度：0.7

  解析

• 6．在△ABC中，∠B=90°，AB=4，BC=8，D為△ABC所在平面上的一點，

  BD

  =

  5

  ，則

  CD

  ?

  AD

  的最大值為（　　）

  A． 6 10 + 5

  B．25

  C． 4 5 + 5

  D． 8 5 + 5
  組卷：105引用：2難度：0.6

  解析

• 7．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的漸近線與⊙M：（x-a）²+（y-

  b

  2

  ）²=

  b

  2

  4

  交于第一象限內的兩點A，B，若△MAB為等邊三角形，則雙曲線的離心率e=（　　）

  A． 3

  B． 2 3 3

  C．2

  D． 2 3
  組卷：112引用：4難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．

• 21．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的上頂點為M（0，2），右頂點為N，直線MN的斜率為-

  3

  3

  ，A，B，C，D是橢圓上4個點（異于點M），AB∥CD，直線MA與MB的斜率之積為-

  1

  3

  ，直線MC與MD的斜之和為1．
  （1）證明：A，B關于原點對稱；
  （2）求直線AB與CD之間的距離的取值范圍．
  組卷：99引用：1難度：0.4

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  e

  x

  x

  -

  e

  ．
  （1）求f（x）的單調區間和極值；
  （2）若

  g

  （

  x

  ）

  =

  x

  e

  x

  2

  -

  a

  2

  x

  +

  1

  -

  2

  e

  -

  b

  2

  lnx

  -

  1

  有零點，求a²+b²的最小值．
  組卷：55引用：2難度：0.4

  解析