2020-2021學年重慶市沙坪壩區南開中學九年級（下）定時診斷數學試卷（十）

一、選擇題：

• 1．若式子

  x

  -

  2

  有意義，則x的值可以是（　　）

  A．3

  B．1

  C．-1

  D．-2
  組卷：156引用：2難度：0.9

  解析

• 2．如圖是某個幾何體的三視圖，判斷這個幾何體是（　　）
  

  A．圓柱

  B．三棱柱

  C．圓錐

  D．三棱錐
  組卷：110引用：2難度：0.6

  解析

• 3．計算（-3a）²正確的是（　　）

  A．-3a2

  B．6a2

  C．-9a2

  D．9a2
  組卷：151引用：4難度：0.8

  解析

• 4．如果一個正多邊形的一個外角是45°，則這個正多邊形的邊數是（　　）

  A．8

  B．7

  C．6

  D．5
  組卷：492引用：8難度：0.9

  解析

• 5．下列命題中是假命題的是（　　）

  A．兩條平行線之間的距離處處相等

  B．同旁內角互補

  C．角平分線上的點到這個角兩邊的距離相等

  D．對角線相等且互相平分的四邊形是矩形
  組卷：102引用：4難度：0.6

  解析

• 6．如圖，在平行四邊形ABCD中，點E在邊AD上，DE：EA=3：2，連接CE交BD于點F，則△DEF的面積與△BCF的面積之比是（　　）

  A．2：5

  B．3：5

  C．4：25

  D．9：25
  組卷：717引用：4難度：0.6

  解析

• 7．實數a,b,c,d在數軸上的對應點的位置如圖所示，則正確的結論是（　　）
  

  A．a＞-4

  B．0＜c＜1

  C．|a|＜|d|

  D．bd＞0
  組卷：142引用：2難度：0.7

  解析

• 8．船工小王駕駛一艘小艇勻速從甲港向乙港航行，離開甲港后不久便發現有重要物品落在甲港，小王馬上駕駛小艇以相同的速度馳回甲港，到達甲港后，因找重要物品耽誤了一段時間，為了按時到達乙港，小王回乙港時，加快了航行速度．則小艇離乙港的距離y與時間t之間的函數關系的大致圖象是（　　）

  A．

  B．

  C．

  D．
  組卷：1512引用：11難度：0.7

  解析

三、解答題：本大題共7小題，每小題10分，共70分．

• 25．如圖，在平面直角坐標系中，拋物線y=ax²+bx-4（a≠0）與x軸交于A、B兩點，與y軸交于點C，連接AC，已知tan∠CAO=2，點B（-4，0）．
  （1）求這個拋物線的解析式；
  （2）在拋物線上B，C兩點間有一動點P，點E為線段AC的中點，連接BE、BP、PC，求四邊形BPCE面積的最大值；
  （3）將拋物線沿射線CA方向平移

  5

  個單位長度得到新拋物線y'，新拋物線y'與原拋物線對稱軸交于點F，點G為直線y=1上的一個動點，H為平面內任意一點，請直接寫出點G的橫坐標，使得以點F，B，G，H為頂點構成的四邊形是以BF為邊的菱形．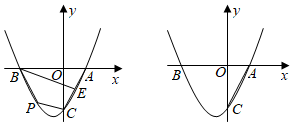
  
  組卷：318引用：3難度：0.3

  解析

四、解答題：本大題1個小題，共8分。必須寫出必要的演算過程或推理步驟，畫出必要的圖形（包括輔助線），請將解答過程寫在答題卡中對應的位置上。

• 26．在等腰Rt△ABC中，∠BAC=90°，AB=AC，延長BA至點D，延長AC至點E，使得BD=AE，DH交BC于點F，過點B作BH⊥BA交DF延長線于點H，連接DE、EH．
  （1）如圖1，若AD=BH，EH=2，DH=2

  2

  ，求點H到DE的距離；
  （2）如圖2，若點F為BC的中點，連接EF，求證：EH=EC+HB；
  （3）如圖3，若AB=2，點N、F分別為線段AC、BC上的點，滿足BF=

  2

  CN，連接FN，將△CFN繞點F順時針旋轉90°，點N旋轉后的對應點為點M，連接AM，直接寫出AM的最小值．
  
  組卷：823引用：3難度：0.1

  解析