2022-2023學年廣東省佛山市南海中學高二（下）期中數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．4名同學參加跑步、跳遠、跳高三個項目，每人限報1項，共有（　　）種報名方法．

  A．64種

  B．81種

  C．32種

  D．12種
  組卷：53引用：3難度：0.6

  解析

• 2．已知實數列-1、x、y、z、-2成等比數列，則xyz=（　　）

  A． 2 2

  B．±4

  C． - 2 2

  D． ± 2 2
  組卷：331引用：6難度：0.8

  解析

• 3．在數列{a_n}中，a₁=1，

  a

  n

  +

  1

  =

  a

  n

  +

  1

  ，則a_n=（　　）

  A．n

  B．n2

  C．n+2

  D． n
  組卷：133引用：3難度：0.7

  解析

• 4．在“全面脫貧”行動中，貧困戶小王2023年1月初向銀行借了扶貧免息貸款10000元，用于自己開發的農產品、土特產品加工廠的原材料進貨，因產品質優價廉，上市后供不應求，據測算：每月獲得的利潤是該月初投入資金的20%，每月底需繳房租800元和水電費400元，余款作為資金全部用于再進貨，如此繼續，預計2023年小王的農產品加工廠的年利潤為（　　）（取1.2¹¹=75，1.2¹²=9）

  A．25000元

  B．26000元

  C．32000元

  D．36000元
  組卷：22引用：1難度：0.6

  解析

• 5．已知函數f（x）=x（x-c）²在x=2處有極大值，則c的值為（　　）

  A．6

  B．6或2

  C．2

  D．4或2
  組卷：172引用：9難度：0.6

  解析

• 6．記數列{a_n}的前n項和為S_n，滿足a₁=1，且na_n+1=（n+1）a_n，則

  2

  S

  n

  +

  10

  n

  的最小值為（　　）

  A． 2 10 + 1

  B． 4 10 + 1

  C． 22 3

  D． 15 2
  組卷：86引用：1難度：0.6

  解析

• 7．已知數列{a_n}的前n項和為S_n，且a₁=1，2S_n=a_n+1a_n，則S₂₀=（　　）

  A．55

  B．50

  C．110

  D．210
  組卷：78引用：3難度：0.6

  解析

三、解答題：本大題共6小題，滿分70分，解答須寫出文字說明、證明過程或演算步驟。

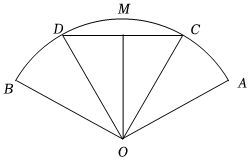• 21．西樵鎮舉辦花市，如圖，有一塊半徑為20米，圓心角

  ∠

  AOB

  =

  2

  π

  3

  的扇形展示臺，展示臺分成了四個區域：三角形OCD擺放菊花“泥金香”，弓形CMD擺放菊花“紫龍臥雪”，扇形AOC和扇形BOD（其中∠AOC=∠BOD）擺放菊花“朱砂紅霜”．預計這三種菊花展示帶來的日效益分別是：泥金香50元/米²，紫龍臥雪30元/米²，朱砂紅霜40元/米²．
  （1）設∠COD=θ，試建立日效益總量y關于θ的函數關系式；
  （2）試探求θ為何值時，日效益總量達到最大值．
  組卷：24引用：3難度：0.5

  解析

• 22．已知函數f（x）=e^-x?sinx,x∈（0，π）．
  （1）求函數f（x）的單調區間；
  （2）若x₁≠x₂，且f（x₁）=f（x₂），證明：

  x

  1

  +

  x

  2

  ＞

  π

  2

  ．
  組卷：41引用：1難度：0.6

  解析