當前位置：試卷中心 > 試卷詳情

2023-2024學年廣東省深圳市南山區南頭中學高二（上）期中數學試卷

發布：2024/9/27 13:0:2

一、單選題

1．直線x+
3
y-2=0的斜率為（　　）
A．
π
3
B．
5
π
6
C．
-
3
D．
-
3
3
組卷：348引用：11難度：0.8
解析
2．已知
a
=
（
-
3
，
2
，
5
）
，
b
=
（
1
，
y
,-
1
）
，若
a
⊥
b
，則y=（　　）
A．4 B．6 C．5 D．3
組卷：163引用：13難度：0.8
解析
3．圓（x-1）²+y²=3的圓心坐標和半徑分別是（　　）
A．（-1，0），3 B．（1，0），3 C．
（
-
1
，
0
）
，
3
D．
（
1
，
0
）
，
3
組卷：417引用：21難度：0.9
解析
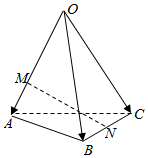4．如圖，空間四邊形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，點M在
OA
上，且OM=2MA，點N為BC中點，則
MN
=（　　）
A．
1
2
a
-
2
3
b
+
1
2
c
B．
-
2
3
a
+
1
2
b
+
1
2
c
C．
1
2
a
+
1
2
b
-
1
2
c
D．
2
3
a
+
2
3
b
-
1
2
c
組卷：2494引用：155難度：0.9
解析
5．如圖，已知直線PM、QP、QM的斜率分別為k₁、k₂、k₃，則k₁、k₂、k₃的大小關系為（　　）
A．k₁＜k₂＜k₃ B．k₁＜k₃＜k₂ C．k₂＜k₁＜k₃ D．k₃＜k₂＜k₁
組卷：397引用：4難度：0.7
解析
6．長方體ABCD-A₁B₁C₁D₁中，AB=BC=1，
A
A
1
=
3
，異面直線AD₁與DB₁所成角的余弦值為（　　）
A．
5
4
B．
5
6
C．
5
5
D．
2
2
組卷：195引用：2難度：0.6
解析
7．設直線l的方程為x-ysinθ+2=0，則直線l的傾斜角α的范圍是（　　）
A．[0，π] B．
[
π
4
，
π
2
]
C．
[
π
4
，
3
π
4
]
D．
[
π
4
，
π
2
）
∪
（
π
2
，
3
π
4
]
組卷：921引用：29難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題

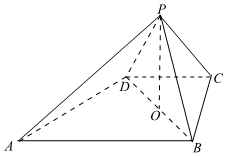21．如圖，在四棱錐P-ABCD中，底面四邊形ABCD為直角梯形，AB∥CD，AB⊥BC，AB=2CD，O為BD的中點，BD=4，PB=PC=PD=
5
．
（1）證明：OP⊥平面ABCD；
（2）若BC=CD，求平面PAD與平面PBC所成銳二面角的余弦值．
組卷：664引用：8難度：0.4
解析
22．如圖，在平面直角坐標系xOy中，已知圓O：x²+y²=4，過點P（0，3），且斜率為k的直線l與圓O交于不同的兩點A，B，點
Q
（
0
，
4
3
）
．
（1）若直線l的斜率
k
=
2
，求線段AB的長度；
（2）設直線QA，QB的斜率分別為k₁，k₂，求證：k₁+k₂為定值，并求出該定值；
（3）設線段AB的中點為M，是否存在直線l使|MO|=
6
3
|MQ|，若存在，求出直線l的方程，若不存在說明理由．
組卷：158引用：4難度：0.6
解析