2022-2023學(xué)年黑龍江省大慶市肇源縣九年級（上）第二次月考數(shù)學(xué)試卷（11月份）（五四學(xué)制）

一、選擇題（3分×10=30分）

• 1．當(dāng)銳角A＞45°時，sinA的值（　　）

  A．小于 2 2

  B．大于 2 2

  C．小于 3 2

  D．大于 3 2
  組卷：264引用：9難度：0.9

  解析

• 2．⊙O的半徑為5，圓心O的坐標(biāo)為（0，0），點P的坐標(biāo)為（4，3），則點P與⊙O的位置關(guān)系是（　　）

  A．點P在⊙O內(nèi)	B．點P在⊙O上
  C．點P在⊙O外	D．點P在⊙O上或⊙O外
  組卷：97引用：1難度：0.9

  解析

• 3．下列對二次函數(shù)y=x²-x的圖象的描述，正確的是（　　）

  A．開口向下

  B．對稱軸是y軸

  C．頂點坐標(biāo)為（ 1 2 ，- 1 4 ）

  D．在對稱軸右側(cè)部分，y隨x的增大而減小
  組卷：767引用：7難度：0.6

  解析

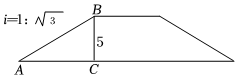• 4．如圖，某地修建的一座建筑物的截面圖的高BC=5m,坡面AB的坡度為1：

  3

  ，則AB的長度為（　　）

  A．10m

  B．10 3 m

  C．5m

  D．5 3 m
  組卷：1993引用：10難度：0.7

  解析

• 5．已知二次函數(shù)y=-

  1

  2

  x²+bx+3，當(dāng)x＞1時，y隨x的增大而減小，則b的取值范圍是（　　）

  A．b≥-1

  B．b≤-1

  C．b≥1

  D．b≤1
  組卷：1239引用：3難度：0.8

  解析

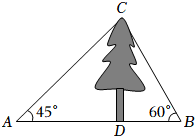• 6．如圖，某數(shù)學(xué)興趣小組測量一棵樹CD的高度，在點A處測得樹頂C的仰角為45°，在點B處測得樹頂C的仰角為60°，且A，B，D三點在同一直線上，若AB=16m,則這棵樹CD的高度是（　　）

  A．8（3- 3 ）m

  B．8（3+ 3 ）m

  C．6（3- 3 ）m

  D．6（3+ 3 ）m
  組卷：2859引用：15難度：0.5

  解析

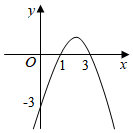• 7．若二次函數(shù)y=ax²+bx+c的圖象如圖所示，則下列說法不正確的是（　　）

  A．當(dāng)1＜x＜3時，y＞0	B．當(dāng)x=2時，y有最大值
  C．圖象經(jīng)過點（4，-3）	D．當(dāng)y＜-3時，x＜0
  組卷：482引用：4難度：0.5

  解析

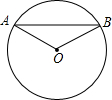• 8．如圖，在半徑為2cm的⊙O中有長為2

  3

  cm的弦AB，則弦AB所對的圓心角的度數(shù)為（　　）

  A．60°

  B．90°

  C．120°

  D．150°
  組卷：216引用：15難度：0.9

  解析

• 9．已知二次函數(shù)y=ax²+bx+c（a≠0，a,b,c為常數(shù)），如果a＞b＞c,且a+b+c=0．則它的圖象可能是（　　）

  A．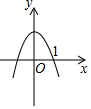

  B．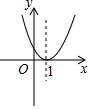

  C．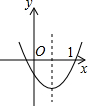

  D．
  組卷：760引用：4難度：0.8

  解析

三．解答題（本題共66分）

• 27．如圖，C為弧AB的中點，OA⊥CD于點M，CN⊥BD于N，且BD為⊙O的直徑，若ON=2，求CD長．
  組卷：173引用：2難度：0.6

  解析

• 28．如圖，拋物線y=ax²+bx+c（a≠0）與直線y=x+1相交于A（-1，0），B（4，n）兩點，且拋物線經(jīng)過點C（5，0）．
  （1）求拋物線的解析式；
  （2）點P是直線AB上方拋物線上的一個動點（不與點A、點B重合），過點P作直線PD⊥x軸于點D，交直線AB于點E，設(shè)點P的橫坐標(biāo)為m.
  ①求線段PE長的最大值，并求此時P點坐標(biāo)；
  ②是否存在點P使△BEC為等腰三角形？若存在，請直接寫出m的值；若不存在，請說明理由．
  組卷：78引用：2難度：0.3

  解析