當前位置：試卷中心 > 試卷詳情

2023-2024學年廣東省廣州市越秀區執信中學高一（上）期中數學試卷

發布：2024/10/18 1:0:1

一、單項選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知全集U=R，集合A={x|3x-6＞0}，B={x|x²-4x+3≤0}，則（?_UA）∩B=（　　）
A．{x|1≤x＜2} B．{x|2＜x≤4} C．{x|1≤x≤2} D．{x|x≥1}
組卷：76引用：3難度：0.7
解析
2．已知命題p：?x∈Q，使得x?N，則?p為（　　）
A．?x?Q，都有x?N B．?x?Q，使得x∈N
C．?x∈Q，都有x∈N D．?x∈Q，使得x∈N
組卷：153引用：6難度：0.8
解析
3．在同一平面直角坐標系中，函數y=a^x（a＞0，且a≠1）與y=x+a-1的圖象可能是（　　）
A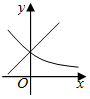． B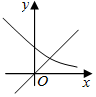． C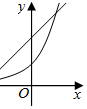． D．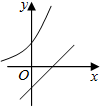
組卷：86引用：2難度：0.7
解析
4．已知函數
f
（
x
）
=
2
x
-
3
，
x
＞
1
x
2
+
1
，
x
≤
1
，則f（f（3））=（　　）
A．2 B．1 C．
1
2
D．
1
4
組卷：36引用：4難度：0.8
解析
5．下列根式與分數指數冪的互化正確的是（　　）
A．
-
x
=
（
-
x
）
1
2
B．
6
y
2
=
y
1
3
（
y
＜
0
）
C．
x
-
1
3
=
1
3
x
（x＞0） D．
[
3
（
-
x
）
2
]
3
4
=
x
1
2
（
x
＞
0
）
組卷：152引用：8難度：0.8
解析
6．流行病學基本參數：基本再生數R₀指一個感染者傳染的平均人數，世代間隔T指相鄰兩代間傳染所需的平均時間．在新冠肺炎疫情初始階段，可用模型：
I
（
t
）
=
N
0
e
rt
（其中N₀是開始確診病例數）描述累計感染病例I（t）隨時間t（單位：天）的變化規律，指數增長率r與R₀，T滿足R₀=1+rT，有學者估計出R₀=3.4，T=6．據此，在新冠肺炎疫情初始階段，當I（t）=2N₀時，t的值為（　　）（ln2≈0.69）
A．1.2 B．1.7 C．2.0 D．2.5
組卷：196引用：10難度：0.6
解析
7．f（x）是定義在R上的函數，
f
（
x
+
1
2
）
+
1
2
為奇函數，則f（2023）+f（-2022）=（　　）
A．-1 B．
-
1
2
C．
1
2
D．1
組卷：504引用：7難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．某中學為了迎接建校100周年校慶，決定在學校校史館利用一側原有墻體，建造一間墻高為3米，底面積為24平方米，且背面靠墻的長方體形狀的榮譽室．由于榮譽室的后背靠墻，無需建造費用．甲乙兩支隊伍參與競標，甲工程隊給出的報價為：榮譽室前面新建墻體的報價為每平方米400元，左右兩面新建墻體報價為每平方米300元，屋頂和地面以及其他報價共計12600元，設榮舉室的左右兩面嬙的長度均為x米（1≤x≤6），乙工程隊給出的整體報價為
1800
a
（
x
+
2
）
x
元（a＞0），綜合考慮各種條件，學校決定選擇報價較低的隊伍施工，如果報價相同，則選擇乙隊伍．
（1）若a=10，問學校該怎樣選擇；
（2）在競爭壓力下，甲工程隊主動降價5400元，若乙工程隊想要確保自己被選中，求實數a的最大值．
組卷：81引用：6難度：0.5
解析
22．對于函數f（x），若在定義域內存在實數x,滿足f（-x）=-f（x），則稱f（x）為“局部奇函數”．
（1）已知二次函數f（x）=ax²+2x-4a,a∈R，試判斷f（x）是否為“局部奇函數”，并說明理由；
（2）若f（x）=4^x-m?2^x+1+m²-1為定義在R上的“局部奇函數”，求函數f（x）在x∈[-1，1]的最小值．
組卷：289引用：4難度：0.5
解析