2021-2022學年江西省宜春市豐城九中日新班高一（下）期末數學試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．

  z

  =

  4

  -

  5

  i

  i

  3

  =（　　）

  A．5+4i

  B．5-4i

  C．-5+4i

  D．-5-4i
  組卷：16引用：2難度：0.8

  解析

• 2．已知集合A={x|x²-8x+7＜0}，B={x|1＜x＜4}，則“x∈A”是“x∈B”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：372引用：4難度：0.8

  解析

• 3．扇形的弧長為12，面積為24，則圓心角的弧度數為（　　）

  A．4

  B．3

  C．2

  D．1
  組卷：480引用：3難度：0.8

  解析

• 4．已知鈍角α的終邊經過點

  （

  cos

  2

  π

  3

  ，

  sin

  π

  6

  ）

  ，則α=（　　）

  A． 2 π 3

  B． 3 π 4

  C． 5 π 6

  D． 7 π 8
  組卷：275引用：3難度：0.8

  解析

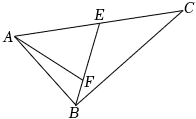• 5．如圖所示，點E為△ABC的邊AC的中點，F為線段BE上靠近點B的四等分點，則

  AF

  =（　　）

  A． 3 8 BA + 5 8 BC

  B． 5 4 BA + 3 4 BC

  C． - 7 8 BA + 1 8 BC

  D． - 3 4 BA + 1 4 BC
  組卷：171引用：5難度：0.7

  解析

• 6．設a=2sin7°cos7°，

  b

  =

  2

  2

  cos

  32

  °

  -

  2

  2

  sin

  32

  °

  ，c=cos75°，則（　　）

  A．a＜b＜c

  B．b＜c＜a

  C．b＜a＜c

  D．c＜a＜b
  組卷：120引用：3難度：0.7

  解析

• 7．若關于x的不等式

  cosx

  +

  sin

  （

  x

  -

  π

  6

  ）

  +

  m

  ≤

  0

  在[0，π]上恒成立，則m的取值范圍為（　　）

  A．（-∞，0]

  B． （ - ∞ ，- 1 2 ]

  C． （ - ∞ ，- 3 2 ]

  D．（-∞，-1]
  組卷：78引用：3難度：0.6

  解析

四、解答題（本大題共6小題，共70分.解答時應寫出必要的文字說明，證明過程或演算.

• 21．已知向量

  m

  =

  （

  sinx

  ,

  1

  ）

  ，

  n

  =

  （

  3

  cosx

  ,-

  1

  2

  ）

  ．令函數

  f

  （

  x

  ）

  =

  （

  m

  +

  n

  ）

  ?

  m

  ．
  （Ⅰ）求函數f（x）的最大值；
  （Ⅱ）△ABC中，內角A，B，C的對邊分別為a,b,c,∠ACB的角平分線交AB于D．其中，函數f（C）恰好為函數f（x）的最大值，且此時CD=f（C），求3a+b的最小值．
  組卷：62引用：3難度：0.6

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  3

  cos

  2

  x

  +

  sin

  2

  x

  +

  1

  ．
  （1）當

  x

  ∈

  [

  -

  π

  4

  ，

  π

  6

  ]

  時，求f（x）的值域；
  （2）若函數

  g

  （

  x

  ）

  =

  f

  （

  -

  a

  2

  x

  +

  π

  4

  ）

  -

  1

  在區間（π，2π）上沒有零點，求正實數a的取值范圍．
  組卷：128引用：2難度：0.5

  解析