2023-2024學年黑龍江省雞西實驗中學高三（上）月考數學試卷（10月份）

一、選擇題（共8小題，每小題5分，滿分40分）

• 1．下列求導運算不正確的是（　　）

  A．（x2）′=2x	B． （ e x + ln 3 ） ′ = e x + 1 3
  C．（3x）′=3xln3	D．（sinx）′=cosx
  組卷：618引用：5難度：0.8

  解析

• 2．已知集合A={x|y=ln（x-1）}，B={x|

  x

  -

  1

  x

  -

  2

  ≤0}，則A∩B=（　　）

  A．{x|1＜x＜2}

  B．{x|1≤x≤2}

  C．{x|1≤x＜2}

  D．{x|1＜x≤2}
  組卷：213引用：3難度：0.8

  解析

• 3．已知

  3

  sinα

  =

  5

  ，

  α

  ∈

  （

  π

  2

  ，

  π

  ）

  ，則

  si

  n

  2

  α

  2

  -

  co

  s

  2

  α

  2

  =（　　）

  A． 2 3

  B． - 2 3

  C．1

  D． - 3 5
  組卷：8引用：3難度：0.8

  解析

• 4．函數

  f

  （

  x

  ）

  =

  3

  x

  -

  3

  -

  x

  2

  ?

  cos

  2

  x

  的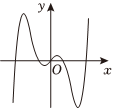部分圖象大致為（　　）

  A．

  B．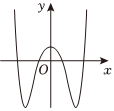

  C．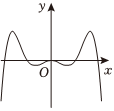

  D．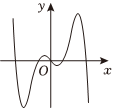
  組卷：69引用：2難度：0.8

  解析

• 5．函數f（x）=x²+lnx-2021的零點個數是（　　）

  A．3

  B．2

  C．1

  D．0
  組卷：64引用：1難度：0.7

  解析

• 6．已知

  sinα

  -

  cosα

  =

  1

  5

  ，

  α

  ∈

  （

  -

  π

  2

  ，

  π

  2

  ）

  ，則

  sinαcosα

  sinα

  +

  cosα

  =（　　）

  A． - 12 5

  B． 12 5

  C． - 12 35

  D． 12 35
  組卷：679引用：3難度：0.7

  解析

• 7．已知定義在R上的奇函數f（x）滿足f（x+2）=-f（x），當x∈[0，1]時，f（x）=2^x-1，則（　　）

  A． f （ 6 ） ＜ f （ - 7 ） ＜ f （ 11 2 ）	B． f （ 6 ） ＜ f （ 11 2 ） ＜ f （ - 7 ）
  C． f （ - 7 ） ＜ f （ 11 2 ） ＜ f （ 6 ）	D． f （ 11 2 ） ＜ f （ - 7 ） ＜ f （ 6 ）
  組卷：782引用：19難度：0.9

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知函數

  f

  （

  x

  ）

  =

  sinxcosx

  -

  3

  co

  s

  2

  x

  +

  3

  2

  ．
  （1）求函數f（x）的單調遞減區間；
  （2）將函數f（x）的圖象上所有點的橫坐標伸長為原來的2倍，縱坐標不變，再將所得圖象向左平移

  π

  6

  個單位，得到函數g（x）的圖象，當

  x

  ∈

  [

  π

  2

  ，

  π

  ]

  時，求函數g（x）的取值范圍．
  組卷：395引用：4難度：0.7

  解析

• 22．已知函數f（x）=x²-（a-2）x-alnx（a∈R）．
  （Ⅰ）求函數y=f（x）的單調區間；
  （Ⅱ）當a=1時，證明：對任意的x＞0，f（x）+e^x＞x²+x+2．
  組卷：291引用：17難度：0.1

  解析