2022-2023學年北京十三中高三（上）開學數學試卷

一、選擇題（共10小題，每小題4分，共40分）

• 1．下列函數中，定義域與值域均為R的是（　　）

  A．y=lnx

  B．y=ex

  C．y=x3

  D． y = 1 x
  組卷：654引用：3難度：0.7

  解析

• 2．若ab＞0，且a＜b,則下列不等式一定成立的是（　　）

  A．a2＜b2

  B． 1 a ＜ 1 b

  C． b a + a b ＞ 2

  D． a + b 2 ＞ ab
  組卷：207引用：5難度：0.7

  解析

• 3．已知函數

  f

  （

  x

  ）

  =

  2 x - 3 ， x ≥ 0 ，

  - 2 x , x ＜ 0 .

  若f（m）=-1，則實數m的值為（　　）

  A．-2

  B． 1 2

  C．1

  D．2
  組卷：417引用：4難度：0.8

  解析

• 4．投擲3枚硬幣，至少有一枚出現正面的概率是（　　）

  A． 3 8

  B． 1 2

  C． 5 8

  D． 7 8
  組卷：115引用：2難度：0.8

  解析

• 5．已知a=log₃2，b=2^0.1，

  c

  =

  1

  3

  ，則（　　）

  A．c＜a＜b

  B．a＜c＜b

  C．c＜b＜a

  D．a＜b＜c
  組卷：314引用：3難度：0.8

  解析

• 6．已知等比數列{a_n}的前3項和為168，a₂-a₅=42，則a₆=（　　）

  A．14

  B．12

  C．6

  D．3
  組卷：5991引用：24難度：0.7

  解析

• 7．函數

  f

  （

  x

  ）

  =

  x

  |

  x

  |

  ?

  3

  x

  的圖象大致為（　　）

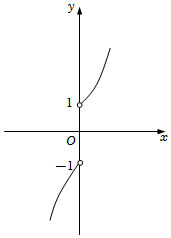
  A．	B．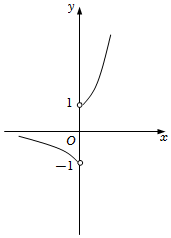
  C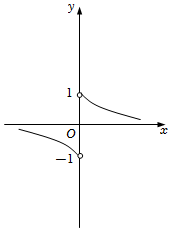．	D．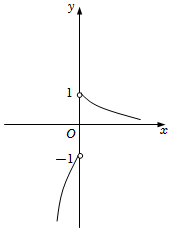
  組卷：558引用：5難度：0.8

  解析

三、解答題（共6小題，共85分，解答應寫出文字說明，演算步驟或證明過程.）

• 20．已知函數f（x）=xlnx+ax²-1，且f′（1）=-1．
  （Ⅰ）求f（x）的解析式；
  （Ⅱ）若對于任意x∈（0，+∞），都有f（x）-mx≤-1，求m的最小值；
  （Ⅲ）證明：函數y=f（x）-xe^x+x²的圖象在直線y=-2x-1的下方．
  組卷：217引用：8難度：0.1

  解析

• 21．若數列{a_n}中存在三項，按一定次序排列構成等比數列，則稱{a_n}為“等比源數列”．
  （1）已知數列{a_n}為4，3，2，1，數列{b_n}為1，2，6，24，分別判斷{a_n}，{b_n}是否為“等比源數列”，并說明理由；
  （2）已知數列{c_n}的通項公式為

  c

  n

  =

  2

  n

  -

  1

  +

  1

  ，判斷{c_n}是否為“等比源數列”，并說明理由；
  （3）已知數列{d_n}為單調遞增的等差數列，且d₁≠0，

  d

  n

  ∈

  Z

  （

  n

  ∈

  N

  *

  ）

  ，求證{d_n}為“等比源數列”．
  組卷：41引用：1難度：0.4

  解析