2022-2023學年江西省南昌二中高二(下)期末數學試卷
發布:2024/6/16 8:0:10
一、單項選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知集合P={x|x2≤4},M={m},若P∩M=M,則m的取值范圍是( )
A.(-∞,-2] B.[-2,2] C.[2,+∞) D.(-∞,-2]∪[2,+∞) 組卷:632引用:5難度:0.7 -
2.已知a,b為實數,則使得“a>b>0”成立的一個充分不必要條件為( )
A. 1a>1bB.ln(a+1)>ln(b+1) C.a3>b3 D. a-1>b-1組卷:347引用:7難度:0.6 -
3.下列函數中為偶函數,且在(0,+∞)上單調遞減的是( )
A.y=(x-2)2 B.y=ln|x| C.y=x?cosx D.y=e-|x| 組卷:35引用:1難度:0.8 -
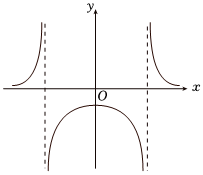 4.函數的圖象如圖所示,則( )f(x)=3+cosxax2-bx+c
4.函數的圖象如圖所示,則( )f(x)=3+cosxax2-bx+cA.a>0,b=0,c<0 B.a<0,b=0,c<0 C.a<0,b<0,c=0 D.a>0,b=0,c>0 組卷:105引用:3難度:0.8 -
5.已知函數
,若f(x1)=f(x2)(其中x1≠x2),則f(x)=log2x2?log2x8的最小值為( )13x1+16x2A. 13B. 213C.4 D.8 組卷:128引用:1難度:0.6 -
6.我們比較熟悉的網絡新詞,有“yyds”、“內卷”、“躺平”等,定義方程f(x)=f'(x)的實數根x叫做函數f(x)的“躺平點”.若函數g(x)=ex-x,h(x)=lnx,φ(x)=2023x+2023的“躺平點”分別為a,b,c,則a,b,c的大小關系為( )
A.a>b>c B.b>a>c C.c>a>b D.c>b>a 組卷:52引用:7難度:0.5 -
7.已知函數f(x)的定義域為R,滿足f(x+1)為奇函數且f(6-x)=f(x),當x∈[1,3]時,f(x)=2x-2x2,則f(2023)=( )
A.10 B.4 C.-4 D. -32組卷:726引用:4難度:0.6
四、解答題:本題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
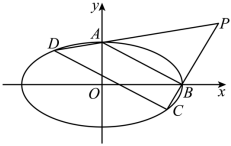 21.已知離心率為的橢圓C:32過點x2a2+y2b2=1(a>b>0),橢圓上有四個動點A,B,C,D,CD∥AB,AD與BC交于P點.如圖所示.(2,3)
21.已知離心率為的橢圓C:32過點x2a2+y2b2=1(a>b>0),橢圓上有四個動點A,B,C,D,CD∥AB,AD與BC交于P點.如圖所示.(2,3)
(1)求曲線C的方程;
(2)當A,B恰好分別為橢圓的上頂點和右頂點時,試探究:直線AD與BC的斜率之積是否為定值?若為定值,請求出該定值;否則,請說明理由;
(3)若點P的坐標為(8,6),求直線AB的斜率.組卷:29引用:1難度:0.5 -
22.已知函數f(x)=axex-(x+1)2(a=R,e為自然對數的底數).
(Ⅰ)討論函數f(x)的單調性;
(Ⅱ)當時,求證:f(x)≥lnx-x2-x-2.a≥1e2組卷:50引用:3難度:0.5


