當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省佛山市順德一中高一（下）期中數學試卷

發布：2024/12/31 2:30:2

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．sin300°的值為（　　）
A．
1
2
B．
-
1
2
C．
3
2
D．
-
3
2
組卷：214引用：3難度：0.8
解析
2．復數z=
2
i
1
-
i
在復平面內對應的點在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：172引用：3難度：0.8
解析
3．已知向量
a
=
（
1
，-
2
）
，
b
=
（
-
2
，
k
）
，且
a
∥
b
，那么實數k=（　　）
A．1 B．-1 C．4 D．-4
組卷：58引用：4難度：0.8
解析
4．已知非零向量
a
，
b
滿足|
a
|=2|
b
|，且（
a
-
b
）⊥
b
，則
a
與
b
的夾角為（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：14782引用：123難度：0.5
解析
5．在△ABC中，內角A，B，C的對邊分別為a,b,c.若△ABC的面積為S，且a=1，4S=b²+c²-1，則△ABC外接圓的面積為（　　）
A．4π B．2π C．π D．
π
2
組卷：552引用：18難度：0.6
解析
6．函數y=tanx+sinx+|tanx-sinx|在區間（
π
2
，
3
π
2
）內的圖象大致是（　　）
A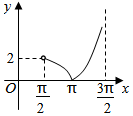． B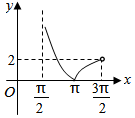． C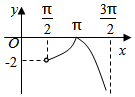． D．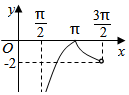
組卷：128引用：14難度：0.7
解析
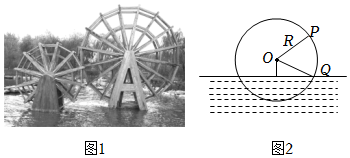7．水車（如圖1）是一種圓形灌溉工具，它是古代中國勞動人民充分利用水力發展出來的一種運轉機械．根據文獻記載，水車大約出現于東漢時期．水車作為中國農耕文化的重要組成部分，體現了中華民族的創造力，為水利研究史提供了見證．圖2是一個水車的示意圖，它的半徑為2m,其中心（即圓心）O距水面1m.如果水車每60s逆時針轉1圈，在水車輪邊緣上取一點P，我們知道在水車勻速轉動時，P點距水面的高度h（單位：m）是一個變量，它是關于時間t（單位：s）的函數．為了方便，不妨從P點位于水車與水面交點Q時開始計時（t=0），則我們可以建立函數關系式h（t）=Asin（ωt+φ）+k（其中A＞0，ω＞0，
-
π
2
＜
φ
＜
0
）來反映h隨t變化的周期規律．下面說法中正確的是（　　）
A．函數h（t）的最小正周期為40
B．
h
（
t
）
=
2
sin
（
π
30
t
-
π
3
）
+
1
C．當t=40時，水車P點離水面最高
D．當t=150時，水車P點距水面2m
組卷：65引用：4難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．某公司要在一條筆直的道路邊安裝路燈，要求燈柱AB與地面垂直，燈桿BC與燈柱AB所在的平面與道路走向垂直，路燈C采用錐形燈罩，射出的光線與平面ABC的部分截面如圖中陰影部分所示．已知
∠
ABC
=
2
3
π
，
∠
ACD
=
π
3
，路寬AD=15米．設
∠
BAC
=
θ
（
π
12
≤
θ
≤
π
6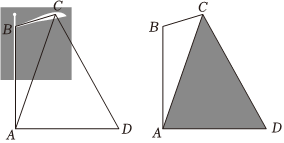
）
．

（1）求燈柱AB的高h（用θ表示）；
（2）此公司應該如何設置θ的值才能使制造路燈燈柱AB與燈桿BC所用材料的總長度最小？最小值為多少？
組卷：65引用：1難度：0.6
解析
22．從①sin²B-sin²A+sin²C-sinBsinC=0，②
bsin
A
+
3
acos
B
=
3
c
，這兩個條件中任選一個，補充在下面問題中，并加以解答．
在△ABC中，a,b,c分別是角A，B，C的對邊，若____．
（1）求角A的大小；
（2）若D是BC的中點，
AD
=
3
，求△ABC面積的最大值；
（3）若O為△ABC的外接圓圓心，且
cos
B
sin
C
AB
+
cos
C
sin
B
AC
=
2
m
AO
，求實數m的值．
組卷：202引用：5難度：0.6
解析