2022年云南省保山市高考數(shù)學(xué)第一次質(zhì)檢試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．集合P={x|0≤x≤3}，Q={x|x²＜9}，則P∩Q=（　　）

  A．{x|0≤x≤3}

  B．{x|0≤x＜3}

  C．{1，2}

  D．{0，1，2}
  組卷：30引用：1難度：0.8

  解析

• 2．已知（1+i）²z=2-2i,其中i是虛數(shù)單位，則復(fù)平面內(nèi)

  z

  +|z|對應(yīng)的點在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：78引用：1難度：0.8

  解析

• 3．已知角θ的終邊過點A（4，a），且sin（θ-π）=

  3

  5

  ，則tanθ=（　　）

  A．- 4 5

  B． 4 5

  C．- 3 4

  D． 3 4
  組卷：146引用：1難度：0.7

  解析

• 4．中國古代張蒼、耿壽昌所撰寫的《九章算術(shù)》總結(jié)了戰(zhàn)國、秦、漢時期的數(shù)學(xué)成就，其中有如下問題：“今有五人分五錢，令上二人所得與下三人等，問各得幾何？”其意思為：“今有5人分5錢，各人所得錢數(shù)依次為等差數(shù)列，其中前2人所得之和與后3人所得之和相等，問各得多少錢？”則中間三人所得錢數(shù)比第1與第5人所得錢數(shù)之和多（　　）

  A． - 1 3 錢

  B． 1 6 錢

  C． 2 3 錢

  D．1錢
  組卷：109引用：1難度：0.7

  解析

• 5．已知函數(shù)f（x）=x³+3x²+ax在x=1處取得極值，若f（x）的單調(diào)遞減區(qū)間為（m,n），n-m=（　　）

  A．5

  B．4

  C．-5

  D．-4
  組卷：128引用：2難度：0.6

  解析

• 6．已知F₁，F(xiàn)₂是離心率等于

  13

  3

  的雙曲線

  C

  ：

  x

  2

  m

  -

  y

  2

  4

  =

  1

  的左、右焦點，過焦點F₂的直線l與雙曲線C的右支相交于A，B兩點，若△ABF₁的周長為20，則|AB|等于（　　）

  A．10

  B．8

  C．6

  D．4
  組卷：88引用：1難度：0.7

  解析

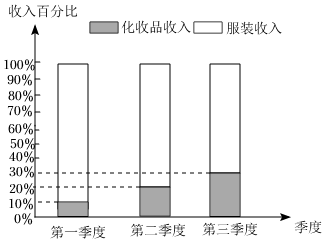• 7．“直播電商”已經(jīng)成為當(dāng)前經(jīng)濟(jì)發(fā)展的新增長點，某電商平臺的直播間經(jīng)營化妝品和服裝兩大類商品，2021年前三個季度的收入情況如圖所示，已知直播間每個季度的總收入都比上一季度的總收入翻一番，則（　　）

  A．該直播間第三季度服裝收入低于前兩個季度的服裝收入之和

  B．該直播間第一季度化妝品收入是第三季度化妝品收入的 1 6

  C．該直播間第二季度化妝品收入是第三季度化妝品收入的 1 3

  D．該直播間第三季度總收入是第一季度總收入的3倍
  組卷：72引用：4難度：0.7

  解析

（二）選考題：共10分．請考生在第22、23題中任選一題作答．如果多做，則按所做的第一題計分．[選修4-4：坐標(biāo)系與參數(shù)方程]

• 22．在平面直角坐標(biāo)系xOy中，點P（1，0）．以原點O為極點，x軸的非負(fù)半軸為極軸建立極坐標(biāo)系．直線l的極坐標(biāo)方程為

  ρsin

  （

  θ

  +

  π

  4

  ）

  =

  2

  2

  ，曲線C的極坐標(biāo)方程為

  ρ

  =

  8

  co

  s

  2

  θ

  2

  -

  4

  ．
  （1）求直線l及曲線C的直角坐標(biāo)方程；
  （2）設(shè)曲線C與直線l交于A，B兩點，求

  1

  |

  PA

  |

  +

  1

  |

  PB

  |

  的值．
  組卷：67引用：1難度：0.7

  解析

[選修4-5：不等式選講]

• 23．已知函數(shù)

  f

  （

  x

  ）

  =

  4

  x

  2

  +

  16

  x

  +

  16

  +

  |

  2

  x

  -

  2

  |

  ．
  （1）求不等式f（x）≤10的解集；
  （2）若對?x∈R，不等式3m≤f（x）總成立，設(shè)M是m的最大值，a+b=M，其中a＞-1，b＞-2，求

  1

  a

  +

  1

  +

  1

  b

  +

  2

  的最小值．
  組卷：33引用：4難度：0.6

  解析