2019-2020學(xué)年北京市人大附中高三（上）統(tǒng)練數(shù)學(xué)試卷（八）

一、選擇題共8小題，每小題5分，共40分．在每小題列出的四個選項中，選出符合題目要求的一項．

• 1．設(shè)全集為R，集合A={x|x²-1＞0}，集合B={y|y=3^x，x∈R}，則A∩B=（　　）

  A．（-∞，-1）

  B．（-∞，-1]

  C．（1，+∞）

  D．[1，+∞）
  組卷：20引用：2難度：0.9

  解析

• 2．直線l與圓x²+y²+2x-4y+1=0相交于A，B兩點，若弦AB的中點（-2，3），則直線l的方程為（　　）

  A．x+y-3=0

  B．x+y-1=0

  C．x-y+5=0

  D．x-y-5=0
  組卷：109引用：12難度：0.9

  解析

• 3．將函數(shù)y=sin（x+

  π

  4

  ）的圖象上各點的縱坐標(biāo)不變，橫坐標(biāo)縮短到原來的

  1

  2

  ，再向右平移

  π

  4

  個單位，所得到的圖象解析式是（　　）

  A．y=sin2x	B．y=sin 1 2 x
  C．y=sin（2x+ π 4 ）	D．y=sin（2x- π 4 ）
  組卷：126引用：8難度：0.9

  解析

• 4．已知方程

  x

  2

  17

  -

  k

  +

  y

  2

  k

  -

  8

  =1表示焦點在x軸上的雙曲線，下列結(jié)論正確的是（　　）

  A．k的取值范圍為8＜k＜17	B．k的取值范圍為k＜8
  C．雙曲線的焦距為10	D．雙曲線的實軸長為10
  組卷：676引用：2難度：0.9

  解析

• 5．在△ABC中，a=8，b=10，△ABC的面積為

  20

  3

  ，則△ABC中最大角的正切值是（　　）

  A． 5 3 3

  B． - 3

  C． - 3 3

  D． 5 3 3 或 - 3
  組卷：22引用：1難度：0.6

  解析

三、解答題共3小題，共30分．解答應(yīng)寫出文字說明，演算步驟或證明過程．

• 16．設(shè)函數(shù)f（x）=x²+ax-lnx（a∈R）．
  （Ⅰ）若a=1，求函數(shù)f（x）的單調(diào)區(qū)間；
  （Ⅱ）若函數(shù)f（x）在區(qū)間（0，1]上是減函數(shù)，求實數(shù)a的取值范圍；
  （Ⅲ）過坐標(biāo)原點O作曲線y=f（x）的切線，證明：切線有且僅有一條，且切點的橫坐標(biāo)恒為1．
  組卷：94引用：4難度：0.3

  解析

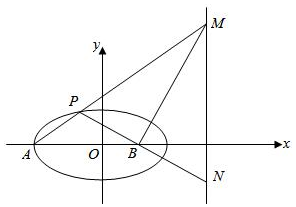• 17．如圖，在平面直角坐標(biāo)系xOy中，橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  3

  2

  ，且過點（1，

  3

  2

  ）．過橢圓C的左頂點A作直線交橢圓C于另一點P，交直線l：x=m（m＞a）于點M．已知點B（1，0），直線PB交l于點N．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）若MB是線段PN的垂直平分線，求實數(shù)m的值．
  組卷：126引用：2難度：0.5

  解析