2023年浙江省寧波市鄞州區藝術實驗學校中考數學一模試卷
發布：2024/5/5 8:0:9
一．選擇題（每小題4分，共40分，在每小題給出的四個選項中，只有一項符合題目要求）
-
1．2023的相反數是（ ）
組卷：5365引用：291難度：0.8 -
2．北京時間2022年11月21日0點，萬眾矚目的卡塔爾世界杯全面打響，據統計在小組賽的賽程中，場均觀看直播人數達到了7062萬人，則7062萬用科學記數法表示為（ ）
組卷：312引用：8難度：0.7 -
3．下列運算正確的是（ ）
組卷：65引用：1難度：0.7 -
4．搶微信紅包已成為中國傳統節日人們最喜愛的祝福方式，今年端午節期間，某人在自己的微信群中發出紅包，一共有10名好友搶到紅包，搶到紅包的金額情況如表：
則10名好友搶到金額的眾數、中位數分別是（ ）金額（元） 4 4.5 5 5.5 6 8 人數（人） 1 3 2 1 2 1 組卷：312引用：7難度：0.9 -
5．將一個正方體截一個角，得到如圖所示的幾何體，則這個幾何體的俯視圖是（ ）組卷：2004引用：13難度：0.9 -
6．下列選項中，可以用來說明命題“兩個銳角的和是鈍角”是假命題的例子是（ ）
組卷：176引用：2難度：0.7 -
7．已知圓錐的底面半徑為9cm,高線長為12cm,則圓錐的側面積為（ ）
組卷：182引用：2難度：0.9 -
8．《九章算術》是我國東漢初年編訂的一部數學經典著作．在它的“方程”一章里，一次方程組是由算籌布置而成的．《九章算術》中的算籌圖是豎排的，為看圖方便，我們把它改為橫排，如圖1、圖2．圖中各行從左到右列出的算籌數分別表示未知數x,y的系數與相應的常數項．把圖1所示的算籌圖用我們現在所熟悉的方程組形式表述出來，就是
，類似地，圖2所示的算籌圖我們可以表述為（ ）3x+2y=19x+4y=23
組卷：203引用：6難度：0.7
三．解答題（本題共8小題，共80分，其中17、20、21題各8分，18題9分，19題10分，22題11分，23題12分，24題14分）
-
23．（1）特殊發現
如圖1，正方形BEFG與正方形ABCD的頂點B重合，BE、BG分別在BC、BA邊上，連接DF，則有：
①=； ②直線DF與直線AG所夾的銳角等于 度；DFAG
（2）理解運用
將圖1中的正方形BEFG繞點B逆時針旋轉，連接DF、AG，
①如圖2，（1）中的結論是否仍然成立？請說明理由；
②如圖3，若D、F、G三點在同一直線上，且過AB邊的中點O，BE=4，直接寫出AB的長 ；
（3）拓展延伸
如圖4，點P是正方形ABCD的AB邊上一動點（不與A、B重合），連接PC，沿PC將△PBC翻折到△PEC位置，連接DE并延長，與CP的延長線交于點F，連接AF，若AB=4PB，則的值是否是定值？請說明理由．DEEF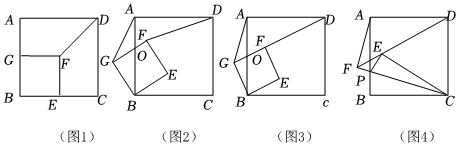
組卷：1031引用：4難度：0.2 -
24．如圖，AB為⊙O的直徑，弦CD⊥AB于點E，G為劣弧AD上一動點，AG與CD的延長線交于點F，連接AC、AD、CG、DG．tan∠DGF=m（m為常數，且m＞1）．
（1）求證：∠AGC=∠DGF；
（2）求的值（用含m的式子表示）；AG?AFCE2
（3）設∠GDC-∠GCD=α，∠F=β．
①求α與β的數量關系；
②當α=90°，且S△CAG=S△CAD時，求m的值．組卷：1394引用：3難度：0.3