2021-2022學年湖北省襄陽市高二（下）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．若函數y=f（x）在x=x₀處的導數為1，則

  lim

  Δ

  x

  →

  0

  f

  （

  x

  0

  +

  2

  Δ

  x

  ）

  -

  f

  （

  x

  0

  -

  Δ

  x

  ）

  Δ

  x

  =（　　）

  A．2

  B．3

  C．-2

  D．-3
  組卷：134引用：5難度：0.7

  解析

• 2．已知

  C

  m

  8

  =

  C

  2

  m

  -

  1

  8

  ，則m等于（　　）

  A．1

  B．4

  C．1或3

  D．3或4
  組卷：582引用：3難度：0.9

  解析

• 3．已知一個盒子里裝有大小相同的5個紅球和3個白球，從中依次不放回地取出3個球，則取出的這3個球中所包含白球個數的數學期望是（　　）

  A． 7 8

  B．2

  C．1

  D． 9 8
  組卷：113引用：2難度：0.5

  解析

• 4．若函數f（x）=x³-2cx²+x有極大值點，則實數c的取值范圍為（　　）

  A．[ 3 2 ，+∞）	B．（ 3 2 ，+∞）
  C．（-∞，- 3 2 ]∪[ 3 2 ，+∞）	D．（-∞，- 3 2 ）∪（ 3 2 ，+∞）
  組卷：90引用：2難度：0.6

  解析

• 5．第24屆冬季奧林匹克運動會在北京舉辦，據此，北京成為世界上第一座雙奧之城，該奧運會激發了大家對冰雪運動的熱情．現將5名志愿者分到3個不同的場所進行志愿服務，要求每個場所至少1人，則不同的分配方案有（　　）

  A．150種

  B．90種

  C．300種

  D．360種
  組卷：80引用：1難度：0.6

  解析

• 6．（x²-x+1）⁵的展開式中，x⁵的系數為（　　）

  A．51

  B．50

  C．-51

  D．-50
  組卷：162引用：3難度：0.6

  解析

• 7．設

  a

  =

  3

  4

  e

  2

  5

  ，

  b

  =

  2

  5

  e

  3

  4

  ，

  c

  =

  3

  5

  ，則（　　）

  A．b＜c＜a

  B．a＜b＜c

  C．c＜b＜a

  D．c＜a＜b
  組卷：466引用：2難度：0.3

  解析

四、解答題：本題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．

• 21．某商場為了考查商場一個月的商品銷售額y（單位：萬元）與廣告費支出x（單位：萬元）之間的相關關系，繪制了如圖散點圖．
  
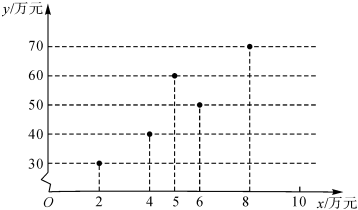
  （1）由散點圖求出y關于x的經驗回歸直線方程；
  （2）統計表明，該商場的某款廣告在平臺發布后，其商品日銷售額x（單位：萬元）近似地服從正態分布（5，1.69），商場對員工的獎勵方案如下：若日銷售額不超過2.4萬元，沒有獎勵；若日銷售額超過2.4萬元但不超過6.3萬元，則每人獎勵200元；若日銷售額超過6.3萬元，則每人獎勵500元，試求該商場每名員工單日獲得獎金的數學期望．（答案精確到整數）
  附：參考公式：經驗回歸直線方程=x+的斜率和截距的最小二乘估計分別為：

  ?

  b

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  =

  n

  ∑

  i

  =

  1

  x

  i

  y

  i

  -

  n

  x

  y

  n

  ∑

  i

  =

  1

  x

  2

  i

  -

  n

  x

  2

  ，

  ?

  a

  =

  y

  -

  ?

  b

  x

  ，
  若Z～N（μ，σ²），則P（μ-σ＜Z≤μ+σ）=0.6827，P（μ-2σ＜Z≤μ+2σ）=0.9545，P（μ-3σ＜Z≤μ+3σ）=0.9973．
  組卷：38引用：3難度：0.5

  解析

• 22．已知函數f（x）=ax³+bx²+cx的導函數為h（x），f（x）的圖象在點（-2，f（-2））的切線方程為3x-y+8=0，且

  h

  ′

  （

  -

  2

  3

  ）

  =

  0

  ．
  （1）求函數f（x）的解析式；
  （2）若f（x）≤xe^x-m+x+1對于任意x∈[0，+∞）恒成立，求正實數m的取值范圍．
  組卷：71引用：2難度：0.2

  解析