2020-2021學年福建省福州八中高一（下）周測數學試卷（五）

一、選擇題

• 1．在復平面內，復數z對應的點與1+i對應的點關于實軸對稱，則

  z

  i

  =（　　）

  A．1+i

  B．-1+i

  C．-1-i

  D．1-i
  組卷：159引用：12難度：0.8

  解析

• 2．已知i為虛數單位，在復平面內，復數

  2

  i

  2

  +

  i

  的共軛復數對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：258引用：2難度：0.7

  解析

• 3．復數z滿足（1-2i）z=4+3i,則|z|=（　　）

  A． 5 5

  B． 5

  C．2 5

  D．4 5
  組卷：11引用：1難度：0.8

  解析

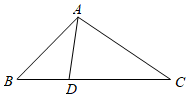• 4．在△ABC中，已知AC=6，

  DC

  =

  2

  BD

  ，

  AD

  ?

  AC

  =

  4

  ，則

  AB

  ?

  AC

  =（　　）

  A．-6

  B．-9

  C．-12

  D．-15
  組卷：252引用：2難度：0.7

  解析

• 5．已知△ABC的內角A，B，C所對的邊分別是a,b,c,且b=2，b²+c²-a²=bc,若BC邊上的中線

  AD

  =

  7

  ，則△ABC的外接圓面積為（　　）

  A．4π

  B．7π

  C．12π

  D．16π
  組卷：1014引用：4難度：0.5

  解析

• 6．我國南宋著名數學家秦九韶發現了由三角形三邊求三角形面積的“三斜求積”公式：設△ABC三個內角A，B，C所對的邊分別為a,b,c,面積為S，則“三斜求積”公式為S=

  1

  4

  [

  a

  2

  c

  2

  -

  （

  a

  2

  +

  c

  2

  -

  b

  2

  2

  ）

  2

  ]

  ．若

  sin

  C

  sin

  A

  =

  c

  2

  5

  ，且（a+b-c）（a-b-c）+4=0，則利用“三斜求積”公式可得△ABC的面積S=（　　）

  A． 3 2

  B．2

  C．4

  D． 3
  組卷：205引用：3難度：0.7

  解析

三、解答題

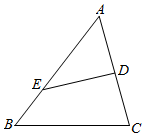• 18．如圖，已知△ABC的內角A，B，C的對邊分別是a,b,c,且asinA+（c-a）sinC=bsinB，點D是AC的中點，DE⊥AC，交AB于點E，且BC=2，DE=

  6

  2

  ．
  （1）求B；
  （2）求△ABC的面積．
  組卷：379引用：11難度：0.5

  解析

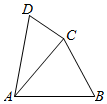• 19．如圖，已知在平面四邊形ABCD中，∠CAB=α，∠ABC=β，∠ACB=γ，且cosγ（sinα+sinβ）=sinγ（2-cosα-cosβ）．
  （1）證明：CA+CB=2AB；
  （2）若CA=CB，DA=2DC=1，求四邊形ABCD的面積的取值范圍．
  組卷：805引用：3難度：0.4

  解析