2023-2024學(xué)年山東省實(shí)驗(yàn)中學(xué)高二（上）開學(xué)數(shù)學(xué)試卷（8月份）（暑假調(diào)研）

一、單項(xiàng)選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的）

• 1．若z（2-i）²=-i（i是虛數(shù)單位），則復(fù)數(shù)z的模為（　　）

  A． 1 2

  B． 1 3

  C． 1 4

  D． 1 5
  組卷：123引用：6難度：0.8

  解析

• 2．如圖所示，△A'O'B'表示水平放置的△AOB的直觀圖，B'在x'軸上，A'O'和x'軸垂直，且A'O'=1，則△AOB的邊OB上的高為（　　）

  A． 4 2

  B．4

  C． 2 2

  D．2
  組卷：225引用：6難度：0.7

  解析

• 3．設(shè)

  a

  =（-1，3），

  b

  =（1，1），

  c

  =

  a

  +k

  b

  ，若

  b

  ⊥

  c

  ，則

  a

  與

  c

  的夾角余弦值為（　　）

  A． 5 5

  B． 2 5 5

  C． 2 3

  D． 2 2 3
  組卷：312引用：3難度：0.6

  解析

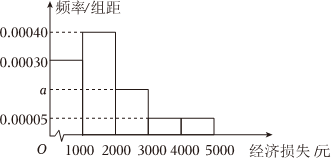• 4．由于受到網(wǎng)絡(luò)電商的沖擊，某品牌的洗衣機(jī)在線下的銷售受到影響，承受了一定的經(jīng)濟(jì)損失，現(xiàn)將A地區(qū)200家實(shí)體店該品牌洗衣機(jī)的月經(jīng)濟(jì)損失統(tǒng)計(jì)如圖所示．估算月經(jīng)濟(jì)損失的平均數(shù)為m,中位數(shù)為n,則

  m

  -

  n

  2

  =（　　）

  A．50

  B．75

  C．90

  D．100
  組卷：25引用：2難度：0.7

  解析

• 5．我國(guó)南宋時(shí)期著名的數(shù)學(xué)家秦九韶在其著作《數(shù)書九章》中，提出了已知三角形三邊長(zhǎng)求三角形的面積的公式，與著名的海倫公式完全等價(jià)，由此可以看出我國(guó)古代已具有很高的數(shù)學(xué)水平，其求法是：“以小斜冪并大斜冪減中斜冪，余半之，自乘于上．以小斜冪乘大斜冪減上，余四約之，為實(shí)．一為從隔，開平方得積．”若把以上這段文字寫成公式，即

  S

  =

  1

  4

  [

  a

  2

  c

  2

  -

  （

  a

  2

  +

  c

  2

  -

  b

  2

  2

  ）

  2

  ]

  ，其中a,b,c分別為△ABC內(nèi)角A，B，C的對(duì)邊．若

  1

  -

  3

  cos

  B

  3

  sin

  B

  =

  1

  tan

  C

  ，b=2，則△ABC面積S的最大值為（　　）

  A． 2

  B． 3

  C．2

  D． 5
  組卷：74引用：2難度：0.7

  解析

• 6．在下列條件中，使M與A，B，C一定共面的是（　　）

  A． OM = OA - OB - OC	B． OM = 1 5 OA + 1 3 OB + 1 2 OC
  C． MA + MB + MC = 0	D． OM + OA + OB + OC = 0
  組卷：1909引用：10難度：0.7

  解析

四、解答題（本大題共4小題，共40分．解答時(shí)應(yīng)寫出必要的文字、證明過(guò)程或演算步驟）

• 19．在四棱錐P-ABCD中，側(cè)面PAD⊥底面ABCD，ABCD為直角梯形，BC∥AD，∠ADC=90°，

  BC

  =

  CD

  =

  1

  2

  AD

  =

  1

  ，PA=PD，E，F(xiàn)為AD，PC的中點(diǎn)．
  （Ⅰ）求證：PA∥平面BEF；
  （Ⅱ）若PC與AB所成角為45°，求PE的長(zhǎng)；
  （Ⅲ）在（Ⅱ）的條件下，求二面角F-BE-A的余弦值．
  組卷：296引用：15難度：0.5

  解析

• 20．在△ABC中，角A、B、C的對(duì)邊分別為a,b,c.
  （1）若（2a-c）cosB=bcosC．b=7，a=5，求sinC的值．
  （2）若△ABC為銳角三角形中，a²+b²=4c²，求cosC的取值范圍．
  組卷：45引用：2難度：0.5

  解析