2022-2023學年湖南省長沙市長沙縣湘郡未來實驗學校九年級（上）入學數學試卷

一、選擇題（共12小題，每小題3分，共計36分）

• 1．下列圖形中，既是中心對稱圖形又是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：153引用：4難度：0.9

  解析

• 2．關于x的方程kx²-4x+4=0有實數根，k的取值范圍是（　　）

  A．k＜1且k≠0

  B．k＜1

  C．k≤1且k≠0

  D．k≤1
  組卷：3151引用：15難度：0.6

  解析

• 3．某商品售價準備進行兩次下調，如果每次降價的百分率都是x,經過兩次降價后售價由298元降到了268元，根據題意可列方程為（　　）

  A．298（1-x2）=268	B．298（1+x）2=268
  C．298（1-2x）=268	D．298（1-x）2=268
  組卷：785引用：7難度：0.7

  解析

• 4．下列說法不正確的是（　　）

  A．點A（-1，2）在第二象限

  B．點P（-2，-3）到y軸的距離為2

  C．若點A（a-1，a-2）在x軸上，則a=1

  D．點A（-3，2）關于原點的對稱點A′的坐標是（3，-2）
  組卷：595引用：6難度：0.8

  解析

• 5．將二次函數y=（x+1）²-2的圖象向右平移2個單位長度，再向下平移3個單位長度得到的二次函數解析式是
  （　　）

  A．y=（x-1）2-5

  B．y=（x-1）2+1

  C．y=（x+3）2+1

  D．y=（x+3）2-5
  組卷：1033引用：11難度：0.6

  解析

• 6．如果二次函數y=ax²+c的圖象如圖所示，那么一次函數y=ax+c的圖象大致是（　　）

  A．

  B．

  C．

  D．
  組卷：2242引用：14難度：0.6

  解析

• 7．如圖，點O為矩形ABCD的對稱中心，點E從點A出發沿AB向點B運動，移動到點B停．延長EO交CD于點F，則四邊形AECF形狀的變化依次為（　　）

  A．平行四邊形→菱形→平行四邊形→矩形

  B．平行四邊形→菱形→正方形→矩形

  C．平行四邊形→正方形→平行四邊形→矩形

  D．平行四邊形→正方形→菱形→矩形
  組卷：319引用：3難度：0.3

  解析

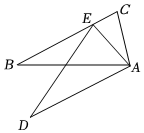• 8．如圖，△ABC中，∠B=35°，∠BAC=70°，將△ABC繞點A旋轉逆時針旋轉α度（0＜α＜180）后得到△ADE，點E恰好落在BC上，則α=（　　）

  A．30°

  B．35°

  C．40°

  D．不能確定
  組卷：1341引用：16難度：0.7

  解析

三、解答題（共8小題，共計66分）

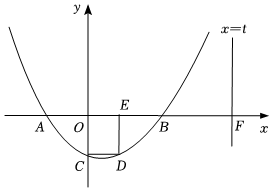• 25．如圖，已知正方形OCDE中，頂點E（1，0），拋物線y=

  1

  2

  x²+bx+c經過點C、點D，與x軸交于A、B兩點（點B在點A的右側），直線x=t（t≠0）交x軸于點F．
  （1）求拋物線的解析式，且直接寫出點A、點B的坐標；
  （2）若點G是拋物線的對稱軸上一動點，且使AG+CG最小，則G點坐標為：

  ；
  （3）在直線x=t（第一象限部分）上找一點P，使得以點P、點B、點F為頂點的三角形與△OBC全等，請你直接寫出點P的坐標；
  （4）點M是射線AC上一點，點N為平面上一點，是否存在這樣的點M，使得以點O、點A、點M、點N為頂點的四邊形為菱形？若存在，請你直接寫出點N的坐標；若不存在，請說明理由．
  組卷：254引用：1難度：0.3

  解析

• 26．在y關于x的函數中，對于實數a,b,當a≤x≤b且b=a+3時，函數y有最大值y_max，最小值y_min，設h=y_max-y_min，則稱h為y的“極差函數”（此函數為h關于a的函數）；特別的，當h=y_max-y_min為一個常數（與a無關）時，稱y有“極差常函數”．
  （1）判斷下列函數是否有“極差常函數”？如果是，請在對應（　　）內畫“√”，如果不是，請在對應（　　）內畫“×”．
  ①y=2x （

  ）；
  ②y=-2x+2 （

  ）；
  ③y=x² （

  ）．
  （2）y關于x的一次函數y=px+q,它與兩坐標軸圍成的面積為1，且它有“極差常函數”h=3，求一次函數解析式；
  （3）若

  -

  1

  +

  13

  2

  ≤

  a

  ≤

  3

  2

  ，當a≤x≤b（b=a+3）時，寫出函數y=ax²-bx+4的“極差函數”h；并求4ah的取值范圍．
  組卷：670引用：2難度：0.2

  解析