2022-2023學年黑龍江省哈爾濱市高一（下）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．若復數z=

  a

  +

  i

  1

  -

  i

  是純虛數，則實數a的值是（　　）

  A．-2

  B．-1

  C．0

  D．1
  組卷：91引用：4難度：0.9

  解析

• 2．某企業職工有高級職稱的共有15人，現按職稱用分層抽樣的方法抽取30人，有高級職稱的3人，則該企業職工人數為（　　）

  A．150

  B．130

  C．120

  D．100
  組卷：155引用：3難度：0.9

  解析

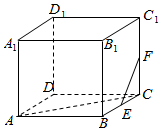• 3．已知正方體ABCD-A₁B₁C₁D₁中，E、F分別為棱BC和棱CC₁的中點，則異面直線AC和EF所成的角為（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：861引用：12難度：0.9

  解析

• 4．設

  e

  1

  ，

  e

  2

  是兩個不共線的向量，若向量

  m

  =

  -

  e

  1

  +

  k

  e

  2

  （

  k

  ∈

  R

  ）

  與向量

  n

  =

  e

  2

  -

  e

  1

  共線，則k=（　　）

  A．0

  B． 1 2

  C．1

  D．2
  組卷：206引用：5難度：0.7

  解析

• 5．拋擲一枚質地均勻的正方體骰子，觀察向上一面的點數，則下列是互斥事件但不是對立事件的是（　　）

  A．“大于3點”與“不大于3點”

  B．“大于3點”與“小于2點”

  C．“大于3點”與“小于4點”

  D．“大于3點”與“小于5點”
  組卷：83引用：5難度：0.8

  解析

• 6．已知三個不同的平面α，β，γ和直線m,n,若α∩γ=m,β∩γ=n,則“α∥β”是“m∥n”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：89引用：6難度：0.7

  解析

• 7．已知平面向量

  a

  =

  （

  1

  ，

  λ

  ）

  ，

  b

  =

  （

  -

  2

  ，

  1

  ）

  ，則下列說法正確的是（　　）

  A．若λ=0，則 | a + b | = 2

  B．若 a ∥ b ，則λ=-2

  C．若 a 與 b 的夾角為鈍角，則λ＜2

  D．若λ=-1，則 a 在 b 上的投影向量為 - 3 5 b
  組卷：116引用：5難度：0.5

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．一只口袋里有形狀、大小、質地都相同的4個小球，這4個小球上分別標記著數字1，2，3，4．甲、乙、丙三名學生約定：
  （i）每人不放回地隨機摸取一個球；
  （ii）按照甲、乙、丙的次序依次摸取；
  （iii）誰摸取的球的數字最大，誰就獲勝．
  用有序數組（a,b,c）表示這個試驗的基本事件，例如：（1，4，3）表示在一次試驗中，甲摸取的球的數字是1，乙摸取的球的數字是4，丙摸取的球的數字是3．
  （1）列出樣本空間，并指出樣本空間中樣本點的總數；
  （2）求甲獲勝的概率；
  （3）寫出乙獲勝的概率，并指出甲、乙、丙三名同學獲勝的概率與其摸取的次序是否有關．
  組卷：12引用：2難度：0.7

  解析

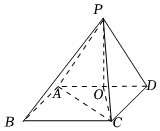• 22．如圖，已知四棱錐P-ABCD的底面為矩形，AB=PD=2，

  AD

  =

  2

  2

  ，O是AD的中點，PO⊥平面ABCD．
  （1）求證：AC⊥平面POB；
  （2）設平面PAB與平面PCD的交線為l.
  （i）求證：l∥AB；
  （ii）求l與平面PAC所成角的大小．
  組卷：167引用：8難度：0.6

  解析