2020-2021學(xué)年江蘇省常州市新北區(qū)西夏墅中學(xué)高二（下）周練數(shù)學(xué)試卷（15）

一、單選題(本大題共8小題，每小題5分，共40分)

• 1．曲線f（x）=lnx-

  1

  x

  在（1，f（1））處的切線方程為（　　）

  A．2x-y-3=0

  B．2x-y-1=0

  C．2x+y-3=0

  D．2x+y-1=0
  組卷：566引用：12難度：0.7

  解析

• 2．設(shè)隨機(jī)變量X服從兩點分布，若P（X=1）-P（X=0）=0.2，則成功概率P（X=1）=（　　）

  A．0.2

  B．0.4

  C．0.6

  D．0.8
  組卷：599引用：5難度：0.9

  解析

• 3．某校甲、乙、丙三位同學(xué)報名參加A，B，C，D四所高校的強(qiáng)基計劃考試，每所高校報名人數(shù)不限，因為四所高校的考試時間相同，所以甲、乙、丙只能隨機(jī)各自報考其中一所高校，則恰有兩人報考同一所高校的概率為（　　）

  A． 1 4

  B． 9 32

  C． 4 9

  D． 9 16
  組卷：144引用：2難度：0.8

  解析

• 4．若函數(shù)f（x）=x²+ax+

  1

  x

  在（

  1

  2

  ，+∞）上是增函數(shù)，則a的取值范圍是（　　）

  A．[-1，0]

  B．[-1，+∞）

  C．[0，3]

  D．[3，+∞）
  組卷：671引用：39難度：0.5

  解析

• 5．已知圓錐的軸截面是邊長為8的等邊三角形，則該圓錐的側(cè)面積是（　　）

  A．64π

  B．48π

  C．32π

  D．16π
  組卷：800引用：11難度：0.7

  解析

• 6．已知函數(shù)f（x）=ax³+bx²+cx（a＜0）的導(dǎo)函數(shù)y=f'（x）的兩個零點為1，2，則下列結(jié)論正確的是（　　）

  A．a(chǎn)bc＜0

  B．f（x）在區(qū)間[0，3]的最大值為0

  C．f（x）有2個零點

  D．f（x）的極大值是正數(shù)
  組卷：15引用：2難度：0.5

  解析

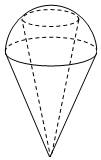• 7．某保鮮封閉裝置由儲物區(qū)與充氮區(qū)（內(nèi)層是儲物區(qū)用來放置新鮮易變質(zhì)物品，充氮區(qū)是儲物區(qū)外的全部空間，用來向儲物區(qū)輸送氮氣從而實現(xiàn)保鮮功能）．如圖所示，該裝置外層上部分是半徑為2半球，下面大圓剛好與高度為3的圓錐的底面圓重合，內(nèi)層是一個高度為4的倒置小圓錐，小圓錐底面平行于外層圓錐的底面，且小圓錐頂點與外層圓錐頂點重合，為了保存更多物品，充氮區(qū)空間最小可以為（　　）

  A．4π

  B． 16 π 3

  C． 28 π 3

  D． 4 π 3
  組卷：245引用：4難度：0.5

  解析

四、解答題(本大題共6小題，第17題10分，18—22題每題12分，共70分)

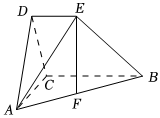• 21．如圖，在四棱錐A-BCDE中，BC∥DE，BC=2DE=2，BC⊥CD，F(xiàn)為AB的中點，BC⊥EF．
  （1）求證：AC⊥BC；
  （2）若AD=CD，AC=2，求直線AE與平面BDE所成角的正弦值的最大值．
  組卷：101引用：2難度：0.5

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  alnx

  +

  1

  x

  （

  a

  ∈

  R

  ）

  ．
  （1）討論函數(shù)f（x）在區(qū)間[1，2]上的最小值；
  （2）當(dāng)a=1時，求證：對任意x∈（0，+∞），恒有

  f

  （

  x

  ）

  ＜

  e

  x

  +

  cosx

  x

  成立．
  組卷：251引用：5難度：0.2

  解析