2002年北京市初二數學競賽（初賽）試卷

一、選擇題（滿分36分）

• 1．

  1

  2002

  +

  1

  3003

  -

  1

  4004

  +

  1

  6006

  -

  1

  8008

  =（　　）

  A． 1 6006

  B． - 3 7007

  C． 5 8008

  D． - 7 9009
  組卷：310引用：3難度：0.9

  解析

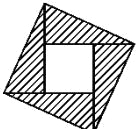• 2．2002年8月在北京召開的國際數學家大會會標如圖所示，它是由四個相同的直角三角形與中間的小正方形拼成的一個大正方形．若大正方形的面積是13，小正方形的面積是1，直角三角形的較長直角邊為a,較短直角邊為b,則a³+b⁴的值為（　　）

  A．35

  B．43

  C．89

  D．97
  組卷：282引用：16難度：0.5

  解析

• 3．若20022002…200215（n個2002）被15整除，則n的最小值等于（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：133引用：1難度：0.5

  解析

• 4．兩個邊長為3，4，5的直角三角形紙片，可以拼成n種不同的凸四邊形，則n的值等于（　　）

  A．6

  B．5

  C．4

  D．3
  組卷：143引用：2難度：0.9

  解析

二、問答題（滿分64分，每小題8分）

• 13．正數m,n滿足m+4

  mn

  -2

  m

  -4

  n

  +4n=3，求

  m

  +

  2

  n

  -

  8

  m

  +

  2

  n

  +

  2002

  的值．
  組卷：797引用：3難度：0.5

  解析

• 14．一個正整數除以5，7，9及11的余數依次是1，2，3，4．求滿足上述條件的最小的正整數．
  組卷：77引用：1難度：0.1

  解析