2022-2023學(xué)年安徽省合肥市廬江縣巢湖七校聯(lián)盟高一（下）期中數(shù)學(xué)試卷

一、單選題（本大題共8小題，共40.0分。在每小題列出的選項(xiàng)中，選出符合題目的一項(xiàng)）

• 1．已知向量

  a

  ，

  b

  ，則“|

  a

  |=|

  b

  |”是“

  a

  =±

  b

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：786引用：7難度：0.8

  解析

• 2．已知

  |

  a

  |

  =3，|

  b

  |=1，

  a

  與

  b

  夾角為120°，則

  a

  +

  b

  在

  a

  上的投影向量為（　　）

  A． - 3 2 b

  B． - 1 2 b

  C． - 1 6 a

  D． 5 6 a
  組卷：178引用：3難度：0.8

  解析

• 3．在等腰三角形ABC中，AB=AC=

  5

  ，BC=2，若P為邊BC上的動(dòng)點(diǎn)，則

  AP

  ?（

  AB

  +

  AC

  ）=（　　）

  A．2

  B．4

  C．8

  D．0
  組卷：343引用：12難度：0.5

  解析

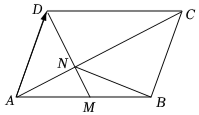• 4．如圖，在平行四邊形ABCD中，M是AB的中點(diǎn)，DM與AC交于點(diǎn)N，設(shè)

  AB

  =

  a

  ，

  AD

  =

  b

  ，則

  BN

  =（　　）

  A． - 2 3 a + 1 3 b

  B． 2 3 a - 1 3 b

  C． - 1 3 a + 2 3 b

  D． 1 3 a - 2 3 b
  組卷：1023引用：15難度：0.8

  解析

• 5．已知在△ABC中，sinA：sinB：sinC=4：3：2，則cosB等于（　　）

  A． 11 16

  B． 7 9

  C． 21 16

  D． 29 16
  組卷：585引用：9難度：0.7

  解析

• 6．已知向量

  a

  =

  （

  λ

  ，

  2

  ）

  ，

  b

  =（2λ，2-4λ），

  m

  =

  a

  +

  b

  ，則

  |

  m

  |

  取最小值時(shí)，實(shí)數(shù)λ的值為（　　）

  A． 6 5

  B． 16 25

  C． 36 25

  D． 28 5
  組卷：76引用：1難度：0.7

  解析

• 7．已知O，N，P在△ABC所在平面內(nèi)，且|

  OA

  |

  =

  |

  OB

  |

  =

  |

  OC

  |

  ，

  NA

  +

  NB

  +

  NC

  =

  0

  ，且

  PA

  ?

  PB

  =

  PB

  ?

  PC

  =

  PC

  ?

  PA

  ，則點(diǎn)O，N，P依次是△ABC的（　　）

  A．重心 外心 垂心	B．重心 外心 內(nèi)心
  C．外心 重心 垂心	D．外心 重心 內(nèi)心
  組卷：1192引用：47難度：0.7

  解析

四、解答題（本大題共6小題，共70.0分。解答應(yīng)寫(xiě)出文字說(shuō)明，證明過(guò)程或演算步驟）

• 21．在△ABC中，角A，B，C的對(duì)邊分別是a,b,c,△ABC的面積為S．
  現(xiàn)有以下三個(gè)條件：
  ①（2c+b）cosA+acosB=0；②sin²B+sin²C-sin²A+sinBsinC=0；③

  a

  2

  -

  b

  2

  -

  c

  2

  =

  4

  3

  3

  S

  ．
  請(qǐng)從以上三個(gè)條件中選擇一個(gè)填到下面問(wèn)題中的橫線(xiàn)上，并求解．
  已知向量

  m

  =（4sinx,4

  3

  ），

  n

  =（cosx,sin²x），函數(shù)f（x）=

  m

  ?

  n

  -

  2

  3

  ，在△ABC中，

  a

  =

  f

  （

  π

  3

  ）

  ，且____，求2b+c的取值范圍．
  組卷：309引用：10難度：0.5

  解析

• 22．已知向量

  a

  和

  b

  ，

  |

  a

  |

  =

  |

  b

  |

  =

  1

  ，且

  |

  a

  +

  k

  b

  |

  =

  3

  |

  a

  -

  k

  b

  |

  ．
  （1）若

  a

  與

  b

  的夾角為60°，求k的值；
  （2）記

  f

  （

  k

  ）

  =

  a

  ?

  b

  +

  1

  4

  （

  k

  2

  -

  3

  k

  -

  1

  k

  +

  3

  ）

  ，是否存在實(shí)數(shù)x,使得f（k）≥1-tx對(duì)任意的t∈[-1，1]恒成立？若存在，求出實(shí)數(shù)x的取值范圍；若不存在，試說(shuō)明理由．
  組卷：62引用：2難度：0.5

  解析