2022-2023學年山東省青島市市南區琴島學校九年級（下）質檢數學試卷（3月份）

一、選擇題（本題滿分24分，共有8道小題，每小題3分）

• 1．下列四個數中，其倒數是-5的是（　　）

  A．-5

  B．5

  C． - 1 5

  D． 1 5
  組卷：46引用：2難度：0.8

  解析

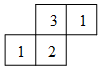• 2．如圖是由幾個小立方塊所搭成的幾何體的俯視圖，小正方形中的數字表示在該位置小立方塊的個數，則這個幾何體的主視圖為（　　）

  A．

  B．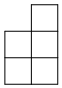

  C．

  D．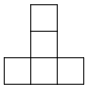
  組卷：248引用：4難度：0.8

  解析

• 3．下列所給圖形中，是中心對稱圖形不是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：58引用：1難度：0.9

  解析

• 4．如果一個圓的直徑是8cm,圓心到一條直線的距離也是8cm,那么這條直線和這個圓的位置關系是（　　）

  A．相離

  B．相交

  C．相切

  D．不能確定
  組卷：145引用：2難度：0.7

  解析

• 5．環境監測中PM_2.5是指大氣中直徑小于或等于2.5微米的顆粒物，也稱為可入肺顆粒物．如果1微米=0.000001米，那么2.5微米用科學記數法可以表示為（　　）米．

  A．2.5×106

  B．2.5×10-5

  C．1.25×10-6

  D．2.5×10-6
  組卷：143引用：3難度：0.9

  解析

• 6．某服裝廠準備加工400套運動裝，在加工完160套后，采用了新技術，使得工作效率比原計劃提高了20%，結果共用了18天完成任務，問計劃每天加工服裝多少套？在這個問題中，設計劃每天加工x套服裝，則根據題意可得方程為（　　）

  A． 160 x + 400 - 160 （ 1 + 20 % ） x =18

  B． 160 x + 400 （ 1 + 20 % ） x =18

  C． 160 x + 400 - 160 20 % x =18

  D． 400 x + 400 - 160 （ 1 + 20 % ） x =18
  組卷：3363引用：36難度：0.9

  解析

• 7．某氣球充滿一定質量的氣體后，當溫度不變時，氣球內的氣體的氣壓P（kPa）是氣體體積V（m³）的反比例函數，其圖象如圖所示，當氣球內的氣壓大于140kPa時，氣球將爆炸，為了安全起見，氣體體積至少為（　　）

  A． 4 5

  B． 5 4

  C． 35 24

  D． 24 35
  組卷：159引用：4難度：0.7

  解析

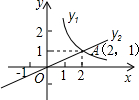• 8．如圖所示，反比例函數y₁與正比例函數y₂的圖象的一個交點坐標是A（2，1），若y₂＞y₁＞0，則x的取值范圍在數軸上表示為（　　）

  A．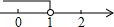

  B．

  C．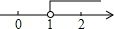

  D．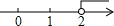
  組卷：358引用：44難度：0.9

  解析

四、解答題（本題滿分74分，共有9道小題）

• 23．閱讀材料：
  大數學家高斯在上學讀書時曾經研究過這樣一個問題：1+2+3+…+100=？經過研究，這個問題的一般性結論是1+2+3+…+n=

  1

  2

  n（n+1），其中n是正整數．
  問題提出：
  在1～n（n≥2）這n個自然數中，每次取兩個數，使得所取兩數之和大于n,共有多少種取法？
  問題解決：
  我們研究數學問題時經常采用“特殊到一般”的解決問題的思想，因此我們首先取幾個特殊值試試．
  （1）在1～5這5個自然數中，每次取兩個數，使得所取兩數之和大于5，共有多少種取法？我們可以這樣來研究：若最小的數取1，則另一個數只能取5，有一種取法；若最小的數取2，則另一個數可以取4、5，有兩種取法；若最小的數取3，則另一個數可以取4、5，有兩種取法；若最小的數取4，則另一個數只能取5，有一種取法；所以共有1+2+2+1=6種取法．
  （2）在1～6這6個自然數中，每次取兩個數，使得所取兩數之和大于6，共有多少種取法？我們可以這樣來研究：若最小的數取1，則另一個數只能取6，有一種取法；若最小的數取2，則另一個數可以取5、6，有兩種取法；若最小的數取3，則另一個數可以取4、5、6，有三種取法；若最小的數取4，則另一個數可以取5、6，有兩種取法；若最小的數取5，則另一個數只能取6，有一種取法；所以共有1+2+3+2+1=9種取法．
  請繼續探究并直接填寫答案：
  （3）在1～7這7個自然數中，每次取兩個數，使得所取兩數之和大于7，共有

  種取法．
  （4）在1～8這8個自然數中，每次取兩個數，使得所取兩數之和大于8，共有

  種取法．
  …
  經過以上嘗試，我們就可以找到問題的答案：
  ①當n為奇數時，在1～n（n≥2）這n個自然數中，每次取兩個數，使得所取兩數之和大于n,共有多少種取法？
  根據前面的探究，我們可以列出算式1+2+3+…

  n

  -

  1

  2

  +

  n

  -

  1

  2

  +…+3+2+1，化簡后，共有

  種取法．
  ②當n為偶數時，在1～n（n≥2）這n個自然數中，每次取兩個數，使得所取兩數之和大于n,共有多少種取法？請你列出算式、化簡并寫出結論．
  新知運用：
  某次知識競賽中，一共有20個小題，對應的分值為1～20分，某選手從中任選兩題，得分高于20分的可能性共有

  種．
  問題拓展：
  各邊長都是整數，最大邊長為12的三角形有多少個？請直接說出答案．
  組卷：244引用：1難度：0.3

  解析

• 24．梯形ABCD中，AD∥BC，∠C=90°，AD=3，CD=4，BC=5，直線MN從AD出發，始終保持與AD平行，并以每秒1個單位的速度向BC移動，交AB于M，交CD于N，同時點P從點C出發，沿CB方向以每秒2個單位速度向點B移動，當P移動到B時，停止運動，同時直線MN也停止運動，設移動時間為t秒，△PMN的面積為S．
  （1）線段AB的長度是

  ；當t=

  時，PN∥AB．
  （2）求面積S與時間t的函數關系式．
  （3）是否存在某一時刻t使得△PMN的面積是梯形ABCD面積的四分之一？若存在，求出此時t的值；若不存在，請說明理由．
  （4）是否存在某一時刻t使得∠MPN是直角？若存在，求出此時t的值；若不存在，請說明理由．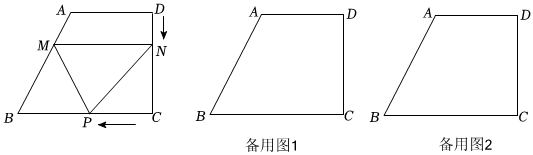
  組卷：150引用：4難度：0.5

  解析