2021-2022學年新疆兵團二中高一（下）期末數學試卷

一、單選題（每小題5分，共40分）

• 1．已知z=1+i,則

  z

  （

  z

  +

  1

  ）

  的模是（　　）

  A． 10

  B．10

  C． 2

  D．2
  組卷：28引用：2難度：0.8

  解析

• 2．設α，β為不重合的平面，m,n為不重合的直線，則其中正確命題的序號為（　　）
  ①m∥α，α∥β，則m∥β；
  ②m?α，n?β，α∥β，則m∥n；
  ③m⊥α，n⊥β，α⊥β，則m⊥n；
  ④n?β，m⊥α，m∥n,則α⊥β．

  A．①③

  B．②③

  C．②④

  D．③④
  組卷：447引用：6難度：0.7

  解析

• 3．若兩個向量

  a

  、

  b

  滿足|

  a

  |=1，|

  b

  |=6，

  a

  ?

  b

  =3，則

  a

  與

  b

  的夾角是（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 2
  組卷：194引用：4難度：0.7

  解析

• 4．復數z滿足|z|=1，則|z-1-i|的最大值為（　　）

  A． 2 - 1

  B．1

  C． 2

  D． 2 + 1
  組卷：142引用：5難度：0.8

  解析

• 5．若復數z在復平面內對應的點位于第二象限，則（　　）

  A．z2不可能為純虛數

  B．z2在復平面內對應的點可能位于第二象限

  C．z2在復平面內對應的點一定位于第三象限

  D．z2在復平面內對應的點可能位于第四象限
  組卷：38引用：3難度：0.7

  解析

• 6．袋子中有大小、形狀、質地完全相同的4個小球，分別寫有“風”、“展”、“紅”、“旗”四個字，若有放回地從袋子中任意摸出一個小球，直到寫有“紅”、“旗”的兩個球都摸到就停止摸球．利用電腦隨機產生1到4之間取整數值的隨機數，用1，2，3，4分別代表“風”、“展”、“紅”、“旗”這四個字，以每三個隨機數為一組，表示摸球三次的結果，經隨機模擬產生了以下20組隨機數：
  411   231   324   412   112   443   213   144   331   123
  114   142   111   344   312   334   223   122   113   133
  由此可以估計，恰好在第三次就停止摸球的概率為（　　）

  A． 1 10

  B． 3 20

  C． 1 5

  D． 1 4
  組卷：85引用：6難度：0.8

  解析

• 7．新冠肺炎疫情的發生，我國的三大產業均受到不同程度的影響，其中第三產業中的各個行業都面臨著很大的營收壓力.2020年7月國家統計局發布了我國上半年國內經濟數據，如圖所示，圖1為國內三大產業比重，圖2為第三產業中各行業比重．
  
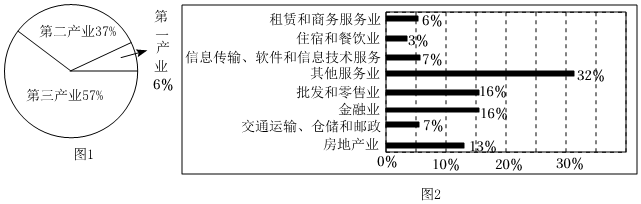
  下列關于我國上半年經濟數據的說法正確的是（　　）

  A．第一產業的生產總值與第三產業中“其他服務業”的生產總值基本持平

  B．第一產業的生產總值超過第三產業中“金融業”的生產總值

  C．若“住宿和餐飲業”生產總值為7500億元，則“房地產”生產總值為22500億元

  D．若“金融業”生產總值為41040億元，則第二產業生產總值為166500億元
  組卷：114引用：3難度：0.8

  解析

四、解答題（共70分）

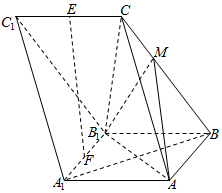• 21．如圖，三棱柱ABC-A₁B₁C₁，側面A₁ABB₁⊥底面ABC，側棱BB₁=2，BA=1，∠ABB₁=60°，點E、F分別是棱C₁C、A₁B₁的中點，點M為棱BC上一點，且滿足AM=

  1

  2

  ，B₁M⊥BC．
  （1）求證：EF∥平面CB₁A；
  （2）求證：AB₁⊥BC；
  （3）求直線BA₁與平面MB₁A所成角的余弦值．
  組卷：576引用：2難度：0.5

  解析

• 22．如圖，平面四邊形ABCD中，BC⊥CD，AB=AD=BC=3，BD=2

  3

  ，以BD為折痕將△ABD折起，使點A到達點P的位置，且PC=

  6

  ．
  （1）若E為棱PD中點，求異面直線CE與PB所成角的余弦值；
  （2）證明：平面BCD⊥平面PBC；
  （3）求二面角P-BD-C的平面角的正弦值．
  
  組卷：527引用：3難度：0.4

  解析