當前位置：試卷中心 > 試卷詳情

2021-2022學年江西省上饒市重點中學協作體高一（下）期末數學試卷

發布：2024/11/2 5:0:2

一、單選題（本題共8小題，每小題5分，共40分.每小題四個選項中，只有一項是最符合題意的.）

1．復數
1
-
i
i
=（　　）
A．-i B．i C．-1-i D．-1+i
組卷：69引用：9難度：0.9
解析
2．已知A為三角形的一個內角，且sinAcosA=-
1
8
，則cosA-sinA的值為（　　）
A．-
3
2
B．±
3
2
C．±
5
2
D．-
5
2
組卷：553引用：7難度：0.9
解析
3．已知
0
＜
A
＜
π
2
，且
tan
A
+
tan
（
A
-
π
4
）
=
2
，則A=（　　）
A．
A
=
π
3
B．
A
=
π
6
C．
A
=
π
4
D．
A
=
π
12
組卷：74引用：2難度：0.7
解析
4．函數
f
（
x
）
=
-
2
sin
（
x
-
π
3
）
在區間（　　）上單調遞增
A．
（
0
，
π
2
）
B．
（
π
，
5
π
3
）
C．
（
2
3
π
，
3
π
2
）
D．
（
3
π
2
，
2
π
）
組卷：227引用：2難度：0.7
解析
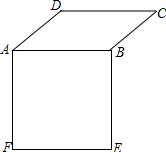5．如圖，在同一平面內沿平行四邊形ABCD邊AB向外作正方形ABEF，其中AB=2，AD=1，∠BAD=
π
4
，則
AC
?
ED
=（　　）
A．-2
2
B．-4+
2
C．0 D．-3+
2
組卷：8引用：2難度：0.7
解析
6．△ABC中，c=
3
，b=1，∠B=30°，則△ABC的面積等于（　　）
A．
3
2
B．
3
4
C．
3
2
或
3
D．
3
2
或
3
4
組卷：74引用：6難度：0.9
解析
7．17世紀法國數學家費馬曾提出這樣一個問題：怎樣在一個三角形中求一點，使它到每個頂點的距離之和最小？現已證明：在△ABC中，若三個內角均小于120°，當點P滿足∠APB=∠APC=∠BPC=120°時，則點P到三角形三個頂點的距離之和最小，點P被人們稱為費馬點．根據以上性質，已知
a
為平面內任意一個向量，
b
和
c
是平面內兩個互相垂直的向量，
|
c
|
=
2
，
|
b
|
=
1
，則
|
a
-
b
|
+
|
a
+
b
|
+
|
a
-
c
|
的最小值是（　　）
A．
2
-
3
B．
2
+
3
C．
3
-
1
D．
3
+
1
組卷：150引用：2難度：0.4
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本題共6小題，共70分.第17題10分，第18-22題各12分，解答應寫出文字說明、證明過程或演算步驟.）

21．已知函數f（x）=
3
sin（ωx+φ）+2sin²（
ωx
+
φ
2
）-2，（ω＞0，0＜φ＜π）的圖象關于直線
x
=
π
6
對稱，且f（x）圖像相鄰的對稱軸之間的距離為
π
2
．
（1）求函數f（x）的解析式；
（2）若f（x）≤t²+t-
1
co
s
2
α
-2tanα-1對任意x∈[-
π
6
，
π
4
]，α∈[-
π
3
，
π
4
]成立，求實數t的取值范圍．
組卷：50引用：3難度：0.7
解析
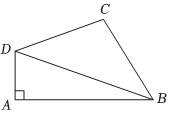22．如圖，在平面四邊形ABCD中，
DC
=
2
AD
=
2
，
∠
BAD
=
π
2
，
∠
BDC
=
π
6
．
（1）若
cos
∠
ABD
=
3
3
，求△ABD的面積；
（2）若∠C=∠ADC，求BC．
組卷：212引用：4難度：0.6
解析