2022-2023學年江蘇省鹽城市鹽都區鹿鳴路中學九年級（上）第一次月考數學試卷

一、選擇題

• 1．半徑為6，圓心角為60°的弧長為（　　）

  A．6

  B．3π

  C．2π

  D．4π
  組卷：557引用：4難度：0.7

  解析

• 2．如圖，從⊙O外一點A引圓的切線AB，切點為B，連接AO并延長交圓于點C，連接BC．若∠A=28°，則∠ACB的度數是（　　）

  A．28°

  B．30°

  C．31°

  D．32°
  組卷：2163引用：16難度：0.8

  解析

• 3．如圖，AB為弦，若∠ABC=30°，弦AC是圓內接正多邊形的一邊，則該正多邊形為（　　）

  A．正十二邊形

  B．正十邊形

  C．正八邊形

  D．正六邊形
  組卷：403引用：1難度：0.6

  解析

• 4．已知⊙O的半徑是一元二次方程x²-2x-3=0的一個根，圓心O到直線l的距離d=4，則直線l與⊙O的位置關系是（　　）

  A．相交

  B．相切

  C．相離

  D．平行
  組卷：1250引用：6難度：0.7

  解析

• 5．如圖為△ABC的內切圓，點D，E分別為邊AB，AC上的點，且DE為⊙I的切線，若△ABC的周長為21，BC邊的長為6，則△ADE的周長為（　　）

  A．15

  B．9

  C．7.5

  D．7
  組卷：786引用：37難度：0.9

  解析

• 6．如圖．將扇形AOB翻折，使點A與圓心O重合，展開后折痕所在直線l與

  ?

  AB

  交于點C，連接AC．若OA=2，則圖中陰影部分的面積是（　　）

  A． 2 π 3 - 3 2

  B． 2 π 3 - 3

  C． π 3 - 3 2

  D． π 3
  組卷：2168引用：15難度：0.5

  解析

三、解答題

• 17．【問題提出】
  我們知道：同弧或等弧所對的圓周角都相等，且等于這條弧所對的圓心角的一半，那么，在一個圓內同一條弦所對的圓周角與圓心角之間又有什么關系呢？
  【初步思考】
  
  （1）如圖1，AB是⊙O的弦，∠AOB=100°，點P₁、P₂分別是優弧AB和劣弧AB上的點，則∠AP₁B=

  °，∠AP₂B=

  °；
  （2）如圖2，AB是⊙O的弦，圓心角∠AOB=m°（m＜180°），點P是⊙O上不與A、B重合的一點，求弦AB所對的圓周角∠APB的度數為

  ；（用m的代數式表示）
  【問題解決】
  （3）如圖3，已知線段AB，點C在AB所在直線的上方，且∠ACB=135°，用尺規作圖的方法作出滿足條件的點C所組成的圖形（①直尺為無刻度直尺；②不寫作法，保留作圖痕跡）；
  【實際應用】
  （4）如圖4，在邊長為12的等邊三角形ABC中，點E、F分別是邊AC、BC上的動點，連接AF、BE，交于點P，若始終保持AE=CF，當點E從點A運動到點C時，點P運動的路徑長是

  ．
  組卷：563引用：3難度：0.5

  解析

• 18．（1）如圖1，在四邊形ABCD中，∠ABC=∠ADC=90°，AD=CD，對角線BD=8，求四邊形ABCD的面積；
  （2）如圖2，園藝設計師想在正六邊形草坪一角∠BOC內改建一個小型的兒童游樂場OMAN．其中OA平分∠BOC，OA=100米，∠BOC=120°，點M，N分別在射線OB和OC上，且∠MAN=90°，為了盡可能的少破壞草坪，要使游樂場OMAN面積最小，你認為園林規劃局的想法能實現嗎？若能，請求出游樂場OMAN面積的最小值；若不能，請說明理由．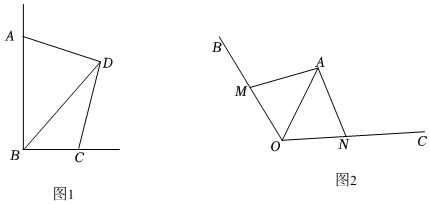
  
  組卷：242引用：2難度：0.2

  解析