2008-2009學年湖南省長沙市長郡中學高三（下）3月短卷訓練數學試卷（文科）（3）

一、選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）．

• 1．設a,b∈R，集合{1，a+b,a}={0，

  b

  a

  ，b}，則b-a=（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：12779引用：64難度：0.9

  解析

• 2．下列函數中，在其定義域內既是奇函數又是減函數的是（　　）

  A．y=-x3，x∈R	B．y=sinx,x∈R
  C．y=x,x∈R	D． y = （ 1 2 ） x ， x ∈ R
  組卷：592引用：82難度：0.9

  解析

• 3．已知tan（α+β）=

  2

  5

  ，tan（β-

  π

  4

  ）=

  1

  4

  ，那么tan（α+

  π

  4

  ）等于（　　）

  A． 13 18

  B． 13 22

  C． 3 22

  D． 1 6
  組卷：883引用：66難度：0.9

  解析

• 4．已知

  a

  ?

  b

  =-12

  2

  ，|

  a

  |=4，

  a

  和

  b

  的夾角為135°，則|

  b

  |為（　　）

  A．12

  B．6

  C． 3 3

  D．3
  組卷：57引用：7難度：0.9

  解析

• 5．已知數列{a_n}，它的前n項和為S_n，若點

  （

  n

  ,

  S

  n

  n

  ）

  恒在直線y=2x+3上，則數列的通項公式a_n=（　　）

  A．4n+1

  B．2n+1

  C．4n-1

  D．2n-1
  組卷：180引用：2難度：0.9

  解析

• 6．已知m,n為直線，α，β為平面，給出下列命題：
  ①

  m ⊥ α

  m ⊥ n

  ?n∥α
  ②

  m ⊥ β

  n ⊥ β

  ?m∥n
  ③

  m ⊥ α

  m ⊥ β

  ?α∥β
  ④

  m ? α

  n ⊥ β

  α ∥ β

  ?m∥n
  其中正確的命題序號是（　　）

  A．③④

  B．②③

  C．①②

  D．①②③④
  組卷：38引用：17難度：0.9

  解析

三、解答題：本大題共4小題，共49分．解答應寫出文字說明，證明過程或演算步驟．

• 18．如圖1，矩形CDEF中DF=2CD=2，將平面ABCD沿著中線AB折成一個直二面角（如圖2），點M在AC上移動，點N在BF上移動，若CM=BN=a（0＜a＜

  2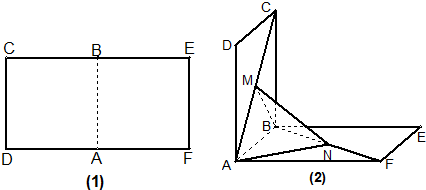

  ）．
  
  （1）求MN的長；
  （2）當a為何值時，MN的長最小；
  （3）當MN長最小時，求面MNA與面MNB所成的鈍二面角α的余弦值．
  組卷：37引用：1難度：0.1

  解析

• 19．已知直線（1+4k）x-（2-3k）y-（3+12k）=0（k∈R）所經過的定點F恰好是橢圓C的一個焦點，且橢圓C上的點到點F的最大距離為8．
  （1）求橢圓C的標準方程；
  （2）已知圓O：x²+y²=1，直線l：mx+ny=1．試證明當點P（m,n）在橢圓C上運動時，直線l與圓O恒相交；并求直線l被圓O所截得的弦長的取值范圍．
  組卷：47引用：10難度：0.5

  解析