2023-2024學年廣西南寧市青秀區翠竹實驗學校八年級（上）期中數學試卷

一、選擇題（共12小題，每小題3分，共36分，在每小題給出的四個選項中只有一項是符合要求的

• 1．2的倒數是（　　）

  A．- 1 2

  B．-2

  C． 1 2

  D．2
  組卷：975引用：44難度：0.9

  解析

• 2．下列圖形中，不是軸對稱的圖形是（　　）

  A．

  B．

  C．

  D．
  組卷：27引用：1難度：0.8

  解析

• 3．現有兩根木棒，長度分別為4cm和9cm,若不改變木棒的長度，要組成一個三角形，應取木棒的長度是（　　）

  A．2cm

  B．5cm

  C．7cm

  D．18cm
  組卷：31引用：1難度：0.6

  解析

• 4．下列計算正確的是（　　）

  A．x4?x4=x16

  B．（a2）3=a6

  C．（2m）3=6m3

  D．（-x2）5=x10
  組卷：110引用：1難度：0.7

  解析

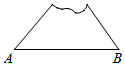• 5．一個缺角的三角形ABC殘片如圖所示，量得∠A=55°，∠B=60°，則這個三角形殘缺前的∠C的度數為（　　）

  A．75°

  B．65°

  C．55°

  D．45°
  組卷：198引用：6難度：0.8

  解析

• 6．已知點P的坐標是（-1，2），點Q與點P關于x軸對稱，則Q的坐標是（　　）

  A．（-1，-2）

  B．（1，2）

  C．（1，-2）

  D．（-2，-1）
  組卷：77引用：1難度：0.9

  解析

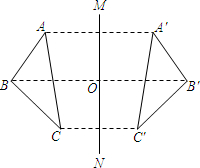• 7．如圖，若△ABC與△A'B'C′關于直線MN對稱，BB'交MN于點O．則下列說法中不一定正確的是（　　）

  A．∠ABC=∠A'B'C′	B．AA'⊥MN
  C．AB∥A′B′	D．BO=B′O
  組卷：1006引用：12難度：0.5

  解析

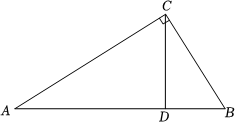• 8．如圖，CD是△ABC的高，∠ACB=90°，若∠A=35°，則∠BCD的度數是（　　）

  A．35°

  B．40°

  C．45°

  D．50°
  組卷：139引用：1難度：0.7

  解析

三、解答題（本大題共8小題，共72分，解答應寫出義字說明、證明過程或演算步驟.）

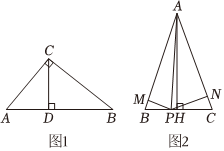• 25．我們發現，“用不同的方式表示同一圖形的面積”可以解決計算線段的有關問題，這種方法稱為等面積法．
  （1）如圖1，BC是AC邊上的高，CD是AB邊上的高，我們知道S_△=

  1

  2

  ×底×高，則

  S

  △

  ABC

  =

  1

  2

  AC

  ?

  BC

  =

  ．
  （2）如圖1，若∠ACB=90°，AC=3，BC=4，AB=5，CD是斜邊AB上的高線．用等面積法求CD的長．
  （3）如圖2，在等腰三角形ABC中，AB=AC=13，BC=10，過A作AH⊥BC于點H，且AH=12，P為底邊BC上的任意一點，過點P作PM⊥AB，PN⊥AC，垂足分別為M，N，連接AP，利用S_△ABC=S_△ABP+S_△ACP，求PM+PN的值．?
  組卷：229引用：1難度：0.3

  解析

• 26．已知△ABC和△ADE都是等邊三角形．
  【模型感知】（1）如圖1，求證：BE=CD；
  【模型應用】（2）如圖2，當點D在CB的延長線上時，求證：AB+BD=BE；
  【類比探究】（3）如圖3，當點D在射線BC上時，過點E作EF⊥AB于點F．猜想線段AB，BF與BD之間存在的數量關系，并證明你的猜想．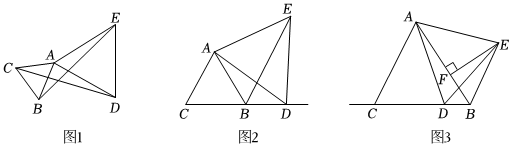
  組卷：696引用：3難度：0.5

  解析